Q&A
お問い合わせの件数が増えてきましたので、回答専用ページを作成しました。 今後メールフォームからのお問い合わせのうち、透視図法に関するご質問等は、こちらに回答させていただきます。 また回答に付随して、スライドやサイト本文を加筆修正すべき場合は、同時に更新作業を行います。
メールフォームはその性質上、問い合わせが一方通行となります。対話形式をご希望の方は返信用のメールアドレスを添えていただくか、ブログのコメント欄をご利用ください。
管理人のリソースには限りがありますので、返答が遅れることや、返答そのものができない場合があります。あらかじめご了承ください。
| お問合せ日 | ご質問の要約 | 回答 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2019/07/31 | 球にパースはかかりますか? またパースがかかる場合、かなり広角な絵でない限りは正円で描いても問題ないでしょうか? |
まず球にパースがかかるか否かというご質問については、「かかります」という回答になります。 詳細は「円 - 球」のページにある通りですが、球は透視図上で、円、楕円、放物線、双曲線のいずれかになります。 平たく言うと、観測者の真正面(視心方向)に球が存在すれば正円として投影され、正面からずれればずれるほど扁平率の大きな楕円(潰れた楕円)になります。 放物線や双曲線になるのは、(視界に対して)非常に大きな球を描く場合に限られます。 | |||||||||
| 2018/08/21 | 誤記について |
「3点透視 - 立方体の描き方」の「立方体の描き方(対角消失点法)」スライドP9の説明文に誤りがありました。 文中の記号VC3は誤りで、正しくはVP3でした。ご指摘いただきありがとうございました。 | |||||||||
| 2018/01/23 | アオリの垂直二点透視について、混合図での仕組みを教えてください。 |
本件は、「2点透視 - 垂直二点透視」に関するお問い合わせです。 2点透視の章では、俯瞰の場合の図のみを示しており、煽り(あおり)の図がありませんでした。申し訳ありません。 おそらくスライドP15に相当する図を煽りについて描けば、分かりやすい説明になるかと思いますが、すぐに作図ができない状況ですので、取り急ぎ参考になりそうな図を挙げておきたいと思います。 「応用 - 消失線とSP」の「1~3点透視図における消失線」にある3番目の図が煽りにおける垂直二点透視の混合図になります。水平線が視心より下に来ることに注意してください。 | |||||||||
| 2017/09/24 | 魚眼グリッドの作図方法を教えてください。 |
本件は、本サイトの参考文献でもある「パース!2 マンガでわかるもっとディープな遠近法」(デヴィッド チェルシー著、マール社)の第6章(P91~106)に記載されている魚眼グリッドの作図方法について、本サイトで解説して欲しいというご依頼です。 この章の内容を掻い摘むと、正射影と等距離射影(書籍上では正距方位と呼ばれています)のそれぞれについて、1~3点透視のグリッドの描き方が説明されています。
時間が取れれば、本サイトでもページを割いてスライドで解説したいと思います。準備が整うまで、しばらくお待ちください。 ※2点透視では左45°右45°、3点透視では左45°右45°俯角(または仰角)35.26°となる向きを指します。
少しだけ解説します。下左図のような表面にグリッドを描いた立方体があるものとします。
他の面の状態を確認するため、灰色の面を外したものが、下右図です。
この立方体の中央にカメラを置くと、透視図法(画角126.87°)では下左図のように見えます。
そして下右図は、魚眼の等距離射影(画角360°)での見え方です。いずれも1点透視です。
書籍P105の中段に描かれている図は、下右図と同じものです。
6面すべてが見えていることに違和感を感じるかもしれませんが、 等距離射影では画角を360°まで広げることができますので、観測者の後方も見えるのです。
今回は図を載せていませんが、正射影では180°が限界画角であるため、観測者の後方は見えません。
つまり灰色の面が全く見えず、赤黄水緑の4面は4マス目までしか見えないことになります。
(カメラを4マス目と同じ奥行に置くため)
下図は2点透視の透視図法(左図)と等距離射影(右図)です。(書籍P105下段)
| |||||||||
| 2017/05/11 | 水平線が傾く場合の作図法について説明してください。特に消失点の取り方の解説をお願いします。 |
まず水平線が傾くとはどういうことなのかを考える必要がありますが、これはカメラを傾けて撮影した場合に相当します。ここでいう傾けるとは、視心方向を軸としてカメラを回転させることを意味します。 このとき、出来上がる写真はカメラを傾けない場合と比べて、写る範囲が違うだけであり、本質的な差異はありません。例えば、カメラを20度傾けて撮影したとすると、出来上がる写真はカメラを傾けずに撮影した写真を20度回転させたものと同一のものです。 (先に述べた通り、長方形の写真では写る範囲が異なるので、その意味では差異があります)
結局のところ、カメラを回転させて撮影しても、写る像としては本質的に同じものですので、透視図法上の作図法は一切変わりありません。つまり水平線が傾かない向きになるまで紙面を回転させた上で、普段通りの作図法を取れば良いことになります。 作図法の具体例としては、「応用 - 消失線とSP」の「消失線の分類とSPの取り方」のスライドP6-9に解説がありますので、そちらを参照してください。 この例では20度傾いた坂道を例にとっていますが、傾きのない普通の地面を20度傾けたカメラで撮影した場合でも、完全に同じ作図手順になります。(世界が傾くこととカメラが傾くことは同義です) 3点透視については、同じスライドのP19以降に解説があります。この例でも消失線は傾きを持ちますが、傾かない向きまで画面を回転させれば、通常の3点透視図と同じ作図法になります。 | |||||||||
| 2017/04/18 | 1点透視や2点透視において、立方体の上面や下面が見えている場合は3点透視になるのではないでしょうか? 上面や下面が見えているということは、すでに目線は完全な水平ではなく傾いているのではないでしょうか? |
1点透視、2点透視、3点透視という分類の定義に関するご質問です。 まずご質問いただいた内容の前半に関する回答ですが、○点透視の○の数と、直方体の見えている面の数には、関係がありません。1点透視で3面見える場合もあれば、3点透視で1面しか見えない場合もあります。直方体の見える面の数については、直方体が消失線を跨ぐか否かだけで分類が可能です。 一般に消失点を覆い隠す配置(=2本の消失線を跨ぐ配置)になっているときは1面しか見えず、1本の消失線を跨ぐ配置の場合は2面見え、それ以外の場合(消失線を跨がない配置の場合)は3面見えます。これは何点透視であっても成り立つ法則です。 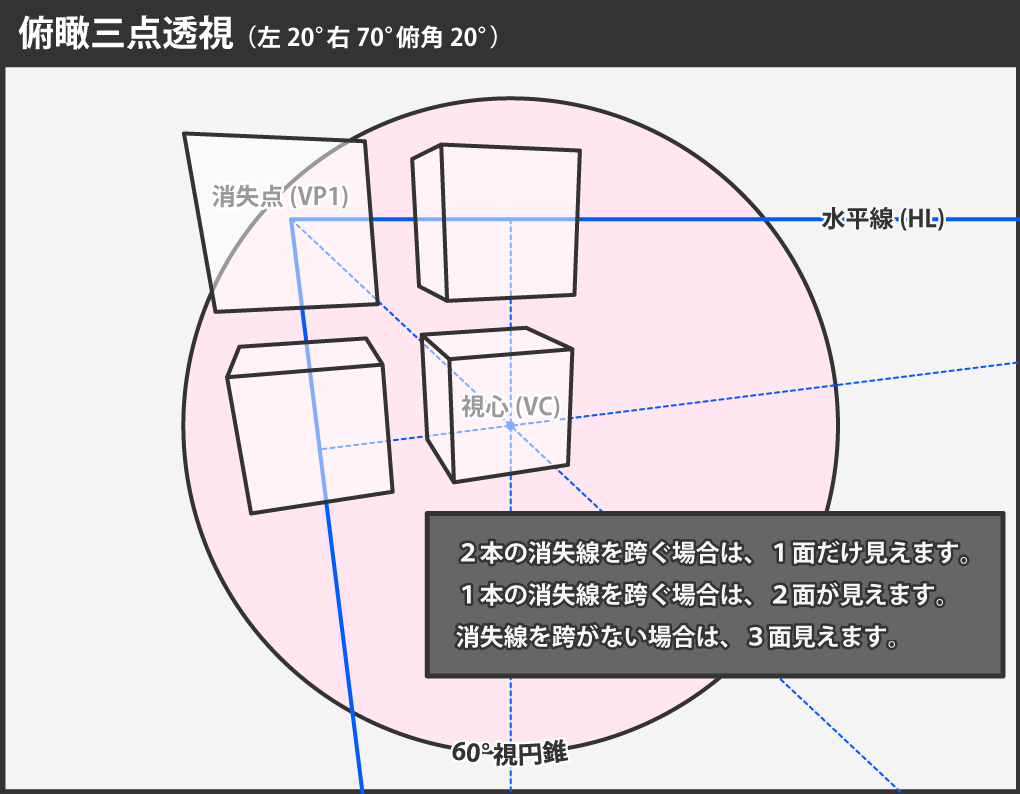
視点を固定した上で、直方体を平行移動させると、消失線をまたぐ際に見える面が変化します。この性質を理解していれば、直方体を画面上のどこに配置すれば見せたい面を見せられるのかという判断ができるようになります。 また消失線から離せば離すほど、面をより広く見せることができます。 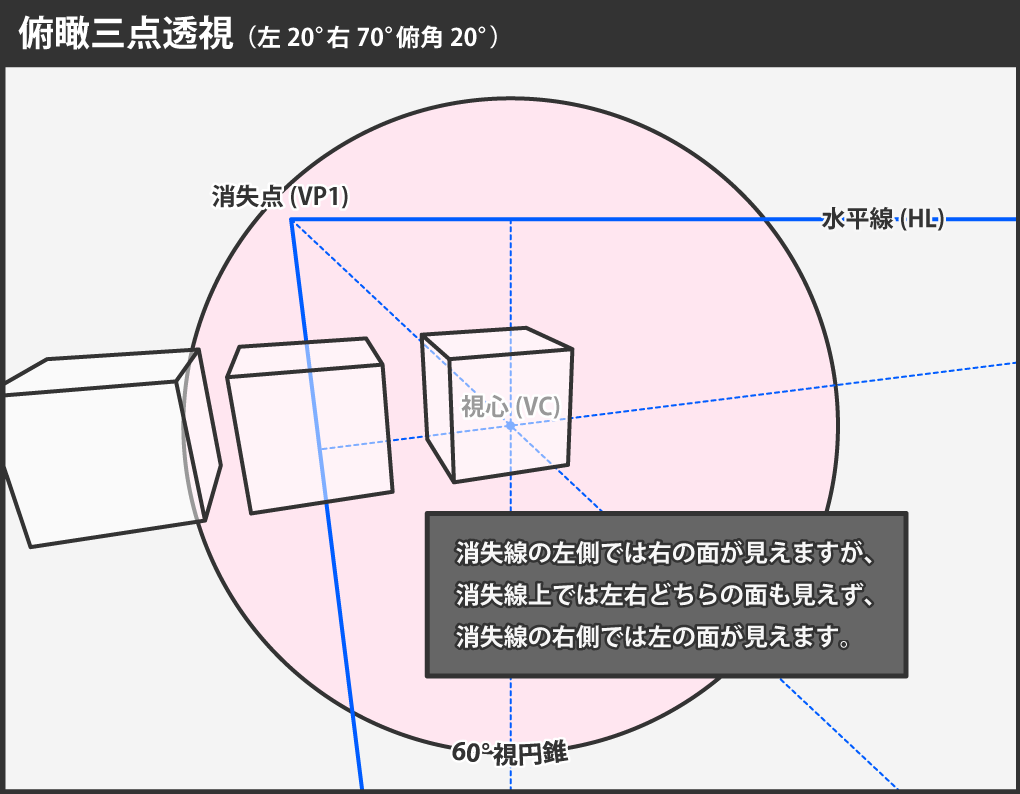
ご質問の後半に関する回答です。人間の視覚はカメラと違って、ある瞬間は非常に狭い範囲しかはっきりと見ることができません。私たちは常に視線移動をすることで、空間の状態を把握しており、これらを無意識のうちに行っているため、なんとなく写真と同じものが見えている気がしていますが、厳密に言えば写真に写っている像のような見え方をしているわけではないです。 写真の場合、カメラを完全な水平方向(地面と平行な方向)に向けた場合であっても、カメラレンズの位置(SP)より斜め上や斜め下を写すことができます。像を写す際にカメラを上下に傾けているわけではないですが、それでも床や天井は像として写ります。 しかし人間の視覚としてはどうでしょうか? 室内で完全に正面を向いたまま、床や天井が見えるでしょうか? ぼやっとなら見えるかもしれません。あるいは部屋が広く、遠くの方であれば見えるかもしれません。しかし通常は首を上下に傾けない限り床や天井ははっきり見えないと思います。 ここがカメラとの違いです。カメラは上下に傾けなくても、床や天井を鮮明に映し出すことができます。 その意味では、人間の視覚は透視図法とは異なると考えた方が無難です。一方、写真や3DCGは透視図法そのものです。 では透視図法は嘘の表現なのかというと、それも違うのです。人間の目が瞬間的に捉えている像をそのまま絵にしても、狭い範囲しか映らないので、絵としては望遠の絵しか描けません。それでは表現に限界がありますので、視線移動を加味した総合的な視覚をなんとか絵に落とし込むしかないのですが、それを機械的に行う方法が透視図法なのです。 世の中にはいろいろな図法がありますが、汎用的に使える方法となると透視図法以外に適当なものが見当たりません。 少し長文になりそうですので、後日ブログの方に内容を整理したエントリを作りたいと思います。公開までしばらくお待ちください。 | |||||||||
| 2017/04/10 | 寸法の測り方のスライドで「23cmの長さが欲しい場合は、23/40を掛ける」という説明がありますが、23cmとは何ですか? また23/40は何に対して掛ければ良いですか? |
本項は「1点透視 - 寸法の測り方」の「画角または90°視円錐を使って、長さを取得する」のスライドP5に関するお問い合わせです。 スライドの解説文は少し分かり難かったかもしれません。申し訳ありません。 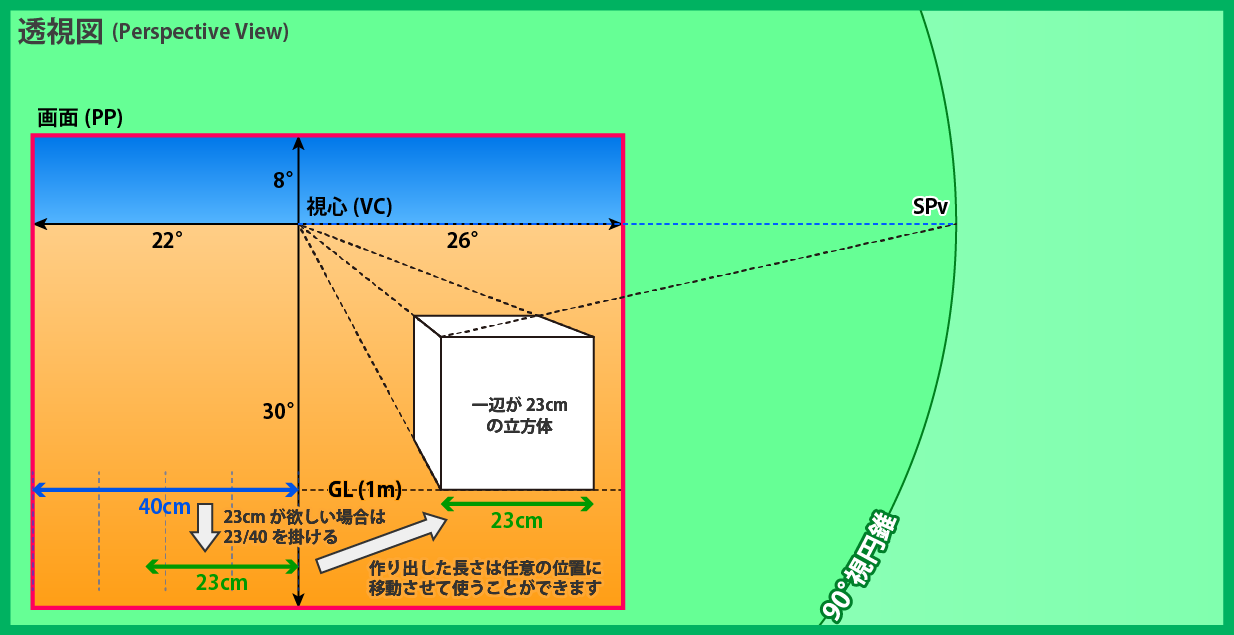
23cmには特別な意味はなく、任意の長さを作り出すことができることの一例として挙げさせていただきました。 上図に示すように、ある長さ(この例では青矢印の40cm)を画面上で取ることができれば、あとは比例計算によって任意の長さを作り出すことができます。 例えば、一辺が23cmの立方体を描きたい場合は、画面上で23cmに相当する長さを取得する必要がありますが、これは緑矢印が示す通り、青矢印の長さを基準として、これに23/40を掛けることで得ることができます。 あとは、これを好きな位置に移動させて箱を描くガイドとして利用します。 | |||||||||
| 2016/09/27 | 観測者と正対していない円が透視図上で正円となる場合がありますが、これは俯瞰一点透視における正円と比べて差異があるのでしょうか? |
本項は「円 - 円の性質1」の「斜円錐の切断」のスライドP6に関するお問い合わせです。 スライドの直後にコラムを2つ追加しましたので、ご覧ください。 | |||||||||
| 2016/08/24 | 視点と立点が同一記号SPで表記されていますが、視点をEye Pointの略であるEPと表記し、両者を区別すればいかがでしょうか? |
ご提案ありがとうございます。ブログの方で回答させていただきましたが、表記の変更は簡単ではなく、また視点に関してはSPの方が一般的な表記であると思われることから、両者を区別せずSPの表記で継続したいと思います。 ただし特に区別が必要なケースにおいては、表記の使い分けを行いたいと思います。 | |||||||||
| 2016/08/20 | 2つの平面が観測者から見て、一方は傾斜があり、一方は水平であるとき、これら2つの平面上に描かれた対角線の消失点が、透視図上で同一円上に乗る理由について説明してください |
本項は「消失点 - 消失線」の消失線のスライドP21において、4点(DP1, DP2, DPs1, DPs2)が VPs を中心とする円上に乗る性質に関するお問い合わせです。
以降の説明を読む前に、必ず上記関連ページのスライドに目を通しておいてください。 透視図法において、空間上の任意の直線に対する消失点の位置を求めるには、その直線と平行な直線をSPを始点として引き、PPとの交点を求めれば良いのでした。そのことを踏まえて、まずは下図1枚目をご覧ください。 傾斜消失点VPsを求めるには、SPを始点として傾斜線と平行な直線を引くことになります。これが下左図Aです。 しかし左図は観測者を含めた空間全体を示す立体的表現であり、透視図ではありません。透視図とはPPを含む平面のことであり、すなわち右図です。 右図上でVPsを作図するには、少々工夫が必要です。左図の三角形SP-VC-VPsは、右方向に90°回転させればPP面上のSPv-VC-VPsの位置に移すことができます。 PP面上に移された三角形は、透視図上に同じ形で描くことができます。このとき、右図のB'は左図のBに対応しており、BはAを回転させたものですから、 3つの線分、A,B,B'は同じ長さになります。 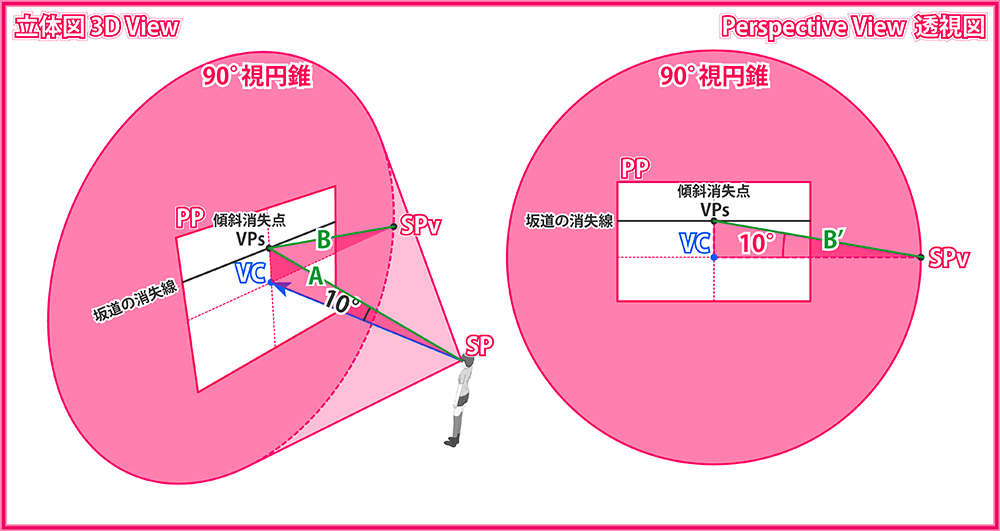
次に坂道の対角線の消失点DPsを、透視図上に作図することを考えましょう。この消失点は観測者から見て45°斜めにありますので、下左図に示す位置にあるはずです。 しかし、このままでは右図に描き入れることができませんので、同じ要領で三角形SP-VPs-DPsを下方向に倒し、PP面まで回転させます。 結果として、三角形はSPs-VPs-DPsに移されます。これを透視図上に描くと右図の通りとなります。 ここで重要なのは、この三角形が直角二等辺三角形であるということです。二等辺三角形の性質から、辺C'とD'は同じ長さであることが保証されます。C'に対応するCはAを回転させたものですから、AとCは同じ長さです。 以上から両図に現れたA,B,C,D,B',C',D'の7辺はすべて同じ長さであることが分かります。 以上を踏まえて、下右図の透視図のみに着目すると、VPsを片端とする3辺B',C',D'は長さが等しいため、各辺の他方の端点であるSPs,SPv,DPsはVPsを中心とする円上に乗ることになります。 ここでSPvはDPと同一の点ですので、結果としてDPsとDPはVPsを中心とする円上の点であることが証明されることになります。 これまでVCより右側についてのみ説明してきましたが、左側についても同じ考察となりますので、冒頭で述べたスライドのDP4点もまた、VPsを中心とする円上に乗ることになります。 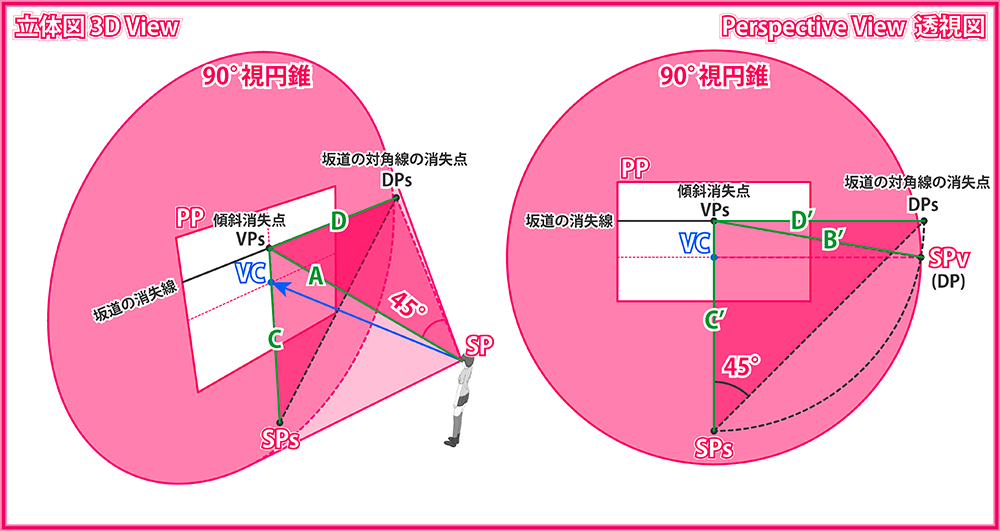
| |||||||||
| 2016/08/20 | (上記質問と関連して)VCおよびVPsを中心とする2つの円について、半径が異なるのは理由があるのでしょうか? |
まず、それぞれの円について補足しておきます。VCを中心とする円は視円錐ですが、VPsを中心とする円は視円錐ではなく特に名称はありません。(単なる作図上の補助円です)。視円錐はその定義上、必ず中心に視心(VC)があります。 両者の円の半径については「VCを中心とする90°視円錐に対して、VPsを中心としDP(対角線の消失点)を通る円の方が常に大きい」という性質があります。傾斜角が10°程度では両者はほぼ同じ大きさですが、傾斜角が大きくなるほどVPsを中心とする円は巨大になっていきます。 その理由は、(上右図において)VCを中心とする90°視円錐は線分DP-VCが半径となるのに対し、VPsを中心とする円は線分DP-VPsが半径となるからです。3点DP-VC-VPsを結ぶ三角形は、∠VCを直角とする直角三角形であり、辺DP-VPsはその斜辺であることから、底辺であるDP-VCよりも必ず長くなります。 | |||||||||
| 2016/04/03 | 2点および3点透視における坂道の対角線の描き方を教えてください |
観測者に対して斜め奥に伸びる坂道に関しては、応用 - 消失線とSPの節をご参照ください。ある平面上の任意の角度の消失点を取るには、その平面の消失線に対応するSPを作図する必要があります。 スライドのP22で45度消失点を求めていますが、グリッドの対角線に対する消失点ではないので注意してください。下図の通り、角VP1-SPs-VP2を2等分する直線を引けば、消失線との交点が対角線の消失点になります。 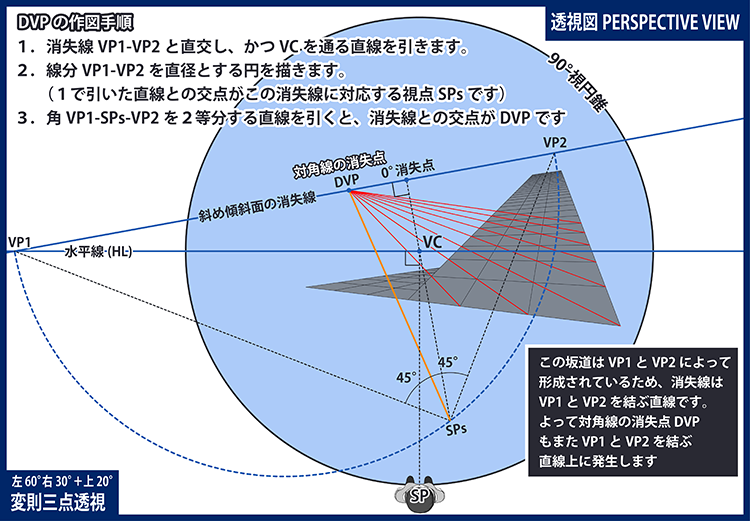
作図理論としては、「2点透視 - 立方体の描き方」の介線法のスライドP21の図が参考になるかもしれません。坂道のグリッドはVP1とVPs2を消失点とする直線群であり、SPから見ると2つの消失点は互いに直交する向きにあります。対角線の消失点はこの角度を2等分する位置にありますので、SPsを使って2つの消失点のなす角を2等分すれば良いことになります。 (下左図ではSPsとDVPを結ぶ直線上にVCが乗っていますが、これは偶然です。作図法は上図を参照してください) 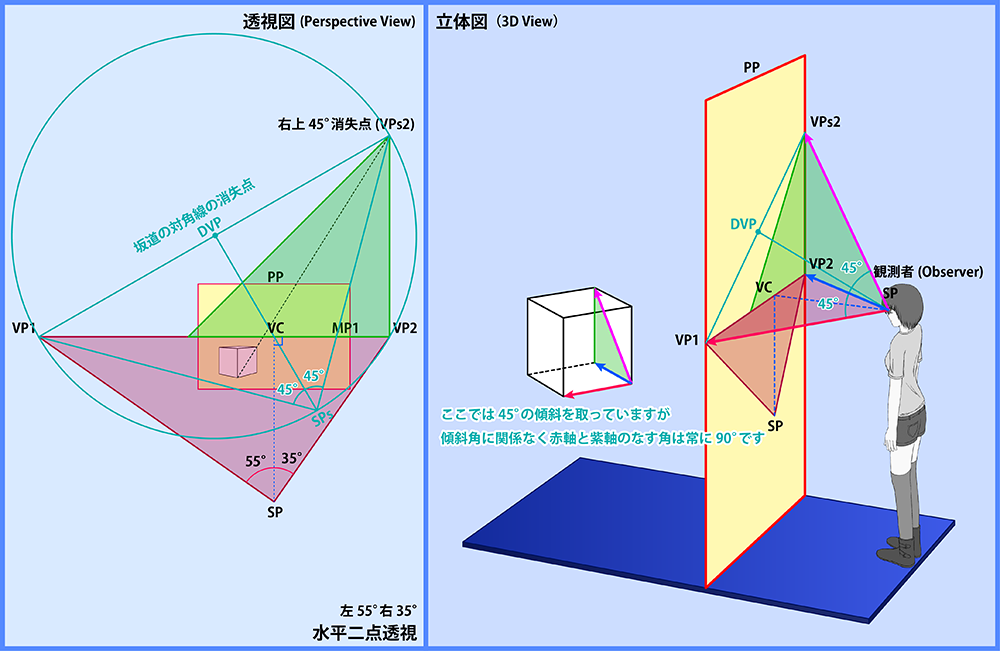
3点透視図上にある坂道の場合も同じ手順で作図できます。下図は透視図法における坂道の分類です。黒い面が傾斜していない地面、その他の色は坂道です。カメラは水平な向きを向いています。坂の上にある不透明の箱は坂に沿って置かれた立方体であり、透明の箱は鉛直方向に真っ直ぐ置かれた側面が平行な六面体です。通常、坂道上の建造物は透明の箱のように建てられます。 今回説明させていただいたのは、下図における赤い坂道になります。 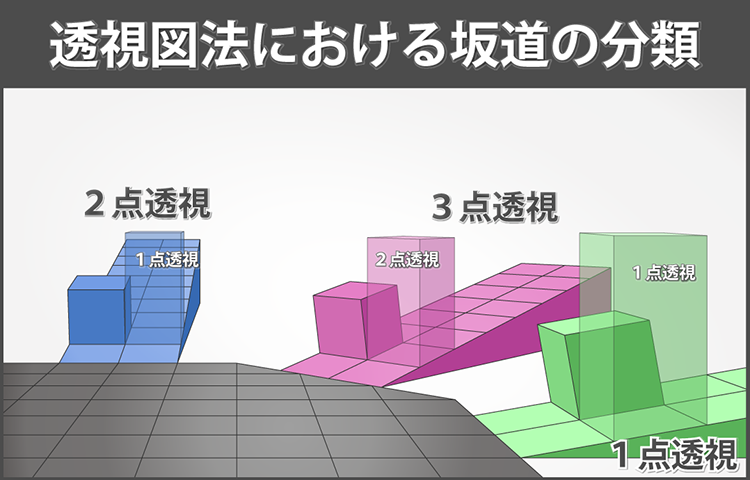
同じ空間を斜め上から見ると、下図のようになります。赤い坂道は例外的に2点透視になるケースを除けば、3点透視になります。つまりベース(透明の箱)が2点透視であっても3点透視であっても、坂道に限れば3点透視になります。(本来、平面自体には○点透視という分類がないので、平面上のグリッドや直方体に対して○点透視と呼ぶべきではありますが) 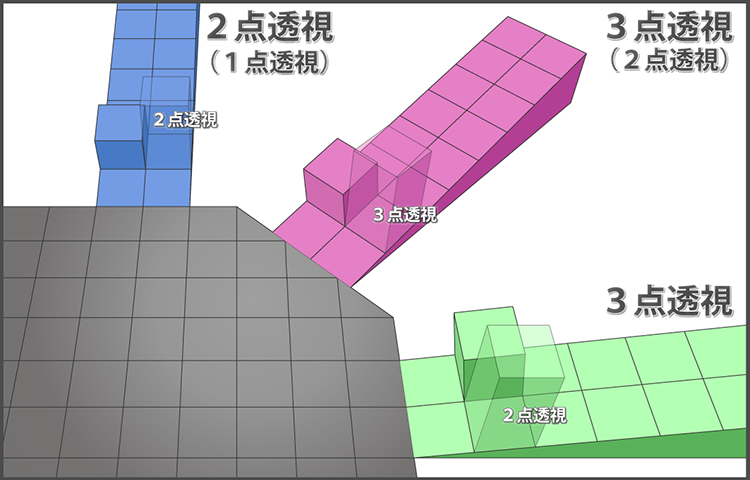
| |||||||||
| 2016/02/01 | 透視図法による影の描き方を教えてください |
陰影の章を追加しましたので、ご覧ください。ソフトを使った方法についてはブログの方で説明させていただきました。透視図法による影の描き方(デジタル) | |||||||||
| 2016/01/13 | 足線法による円の作図方法を教えてください |
円 - 円の描き方にスライドを追加しましたので、ご覧ください。 | |||||||||
| 2015/12/16 | 3点透視の分割・増殖法について教えてください |
3点透視であっても、対角線等を使う通常の分割法が利用できます。ただし3つの軸はすべて消失点に向かう直線であることを忘れないようにしてください。要するに定規の目盛り(物差し)を使って分割してはいけないということです。目盛りのない定規を使うイメージで作図すると間違いを犯さずに済みます。 より汎用的な方法として、基線を使う作図法があります。この方法は消失点を持たない直線(PPと平行な直線)を作図に利用するため、定規の目盛りを使って作図します。 | |||||||||
| 2015/11/30 | 視心(VC)は画面内のどこに置けば良いですか? | 【1次回答】
視心は原則として画面の中央または中央付近に置いてください。3点透視に関しては、無条件で中央に置いても問題ないと思いますが、1点および2点透視では視心は水平線上に置く必要がありますので、水平線自体が画面の縦方向中央を走っていない場合は、若干上下にずれることはやむをえません。水平線が画面外に出てしまうケースでは垂直2点透視または3点透視を使った方が良いでしょう。ブログで実際の絵を使ったより詳細な2次回答をさせていただきましたので、そちらもご参照ください。 |