陰影の発生原理
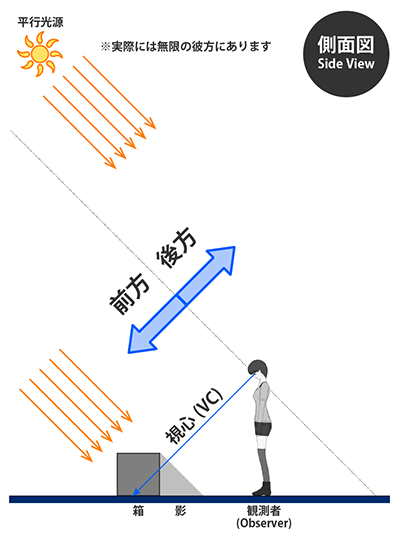
スライドP24の平行光源の作図例に関する補足です。この図における太陽は意外にもカメラの後方にあります。影が手前側に伸びているにも関わらず、光源も手前側にいるという直感的に理解しづらい現象が3点透視図(または垂直2点透視図)の場合は発生しえます。
直線が手前に向かうか奥に向かうかの判定は簡単で、消失点に向かう側が常に奥です。つまりVP1に向かう直線に着目すると、影は消失点から遠ざかる方向に延びていますので、手前側に伸びていると判断できます。一方、太陽光は右下の消失点(消失線VP1-VP3上にあります)に向かっていることから、画面奥に向かって進んでいることが分かります。よって太陽はカメラの後方にいるという結論になります。
※本サイトで言うカメラ後方とは特別な断りがない限り、画角を180°まで広げてもなおかつ画面に入らない領域のことです。人間の感覚でいう後方(地面に立ったときの背中側)ではないので注意してください。
自身が要因となって暗くなる場合を陰と呼びますが、ここでいう自身とは点単位で考えます。例えば腕の影が胴体に落ちるようなケースでは、人間という単位を持ち出して自分自身による「陰」であると判断するのは間違いです。腕と胴体は異なる点なので、胴体に落ちる影は腕を要因としているので「影」が正解です。
3DCGにおいて陰影の判定は陰(shade)の方が圧倒的に簡単であり、影(shadow)の判定には膨大な時間がかかります。なぜなら、陰の判定は自分と光源だけで行えるのに対し、影は空間上に存在するすべてのオブジェクトに対して、影の要因となっているか否かを判定しなければならないからです。
3DCGにおいては陰の描画(シェーディング)と影の描画(シャドウイング)は異なる処理であるため、両者の区別は重要です。 ソフトの設定次第で陰は描くが、影は描かないとなっている場合も往々にしてあるため、異なる2つの概念が存在することはユーザーも知っておく必要があります。
しかし手描きで絵を描く人にとっては、厳密な意味でのシェードとシャドウの違いを区別する必要はないと思われます。 スライドの最後で例示したようなマニアックな分類はできたところで作画上あまり意味はありません。 ただ、大まかな区別ぐらいはできた方が良いでしょう。
影の消失点(まとめ)
以下の法則は光源が点光源、平行光源のいずれであっても成立します。
- 直線状の物体が投影面と平行であるとき、その影は空間的に物体と平行な直線になります。よって透視図上では同一の消失点に収束します。ただし物体である直線が消失点を持たない場合は、影の直線も消失点を持たず、画面上で互いに平行な直線となります。
- 直線状の物体が投影面と平行でないとき、その影もまた空間的に物体と平行でない直線になります。よって透視図上では異なる消失点に収束します。ただし一方または両方が消失点を持たないケースが存在します。
光源を視点とした透視図の活用法
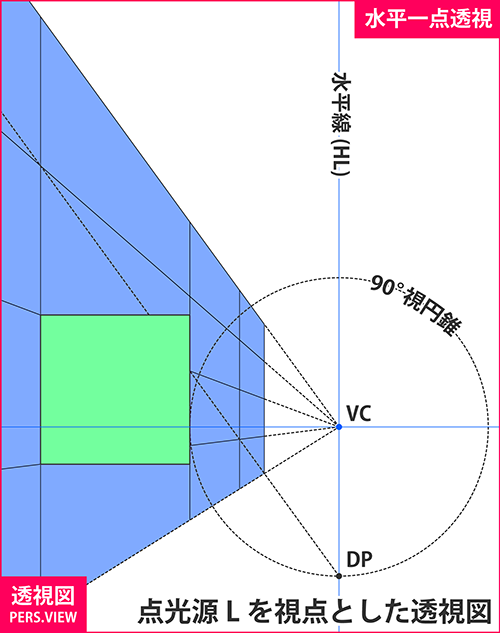
光源を視点とした透視図は周囲のグリッド等と併せて描けば、影を作画する際の大きな助けとなります。 なぜなら、グリッドの目盛りを使っておおよその影の位置を割り出せるからです。 特に人物のような複雑な形状に対する影を描く場合に、この方法は有効です。
ここで問題となるのは視心の向きです。多くの場合、影は地面に付きます。 しかし視心は定義上PPと直交することが決まっていますので、地面を投影面とする限り、視心は必ず真下を向くことになります。 真下方向の透視図(俯瞰一点透視)は普段なじみのない構図であることから、多くの人にとって描きにくいことが予想されます。
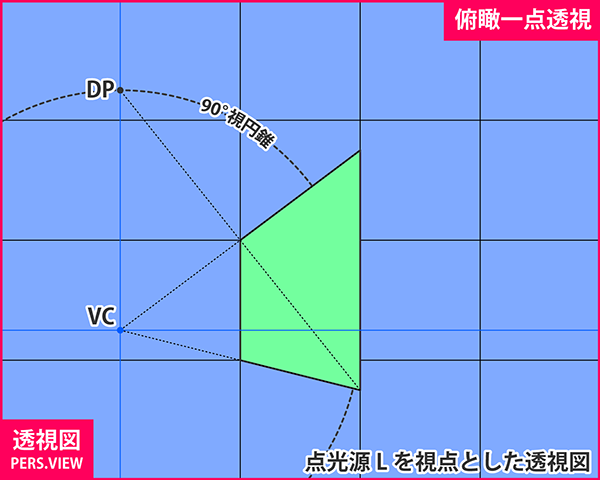
しかし安心してください。影の作画において光源視点の透視図を補助的に使いたい場合は、必ずしも影の投影面をPPとしなくても良いのです。 例えば左上図のように地面と垂直な面をPPとした透視図を描いても、グリッドと影の関係性は完全に正確なものになります。
緑の正方形の4隅の位置が、背後に映るグリッドのどの位置と対応しているかに注目してください。 真上からみた光源視点の透視図(左中図)や本命の透視図の影(左下図)と完全に同じ関係になっていることが確認できます。
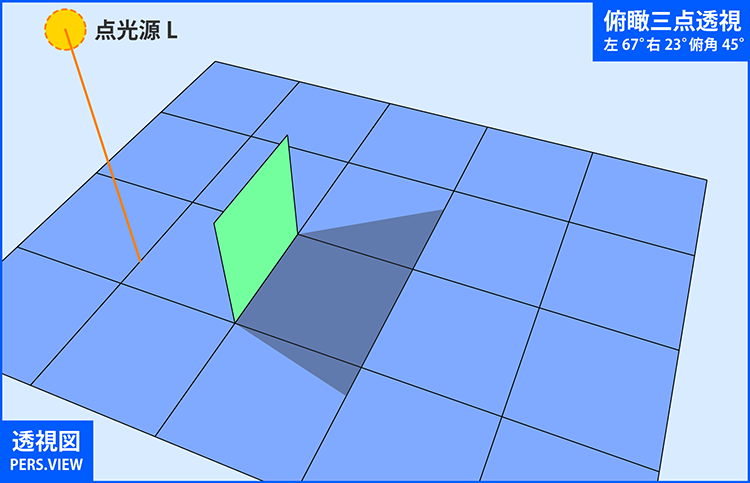
とはいえ、この例において水平の一点透視図で物体を視野に収めるには超広角の絵を描く必要があり、 仮に映っているものが正方形ではなく人物であったとすると、作画の難度が高くなることが予想されます。 画角の問題に関しては、光源と物体の位置関係次第ですので、臨機応変に対応するしかないですが、 この物体配置であれば、45度程度の俯角で見たもの(俯瞰二点透視)を描くのがもっとも楽に描けるのではないかと思います。
結論として、影の対象となる物体が完全に含まれる構図であれば、任意の向きに視心を取ることができます。 影が地面と壁の双方にまたがる場合でも、光源視点の透視図は1枚だけ描けばOKです。
注意を促しておきますが、視心を変更することは許されても、視点を変更することは絶対に許されません。 光源の位置以外を視点に置いた透視図は影の作画において何の役にも立ちません。 これが問題となるのは平行光源の場合です。平行光源において、その投影図は平行投影図になります。 平行投影図には視心という概念自体が存在しませんが、それはともかく影用の図を描く際に視線の向きを変えることができません。 なぜなら平行投影図において視線の向きを変えることは視点を変えることと同義だからです。 平行投影図には本来視点という概念がありませんが、射影幾何学的に考えれば無限遠点が視点になります。 無限遠点には向きという属性があり、向きの異なる無限遠点は異なる点であるため、 視線の向きが異なる平行投影図は、別視点の図ということになります。 よって平行光源においては、その光源が指定する向きから見た絵を描くしかありません。
現実の影との違い
上のスライドでは点光源という理想的な光源を仮定していますが、現実世界には完全な点光源は存在しません。 周囲の物体を見渡してもらうと分かりますが、影の輪郭線はぼけることがあります。これは光源が一定の大きさを持つために起こる現象です。
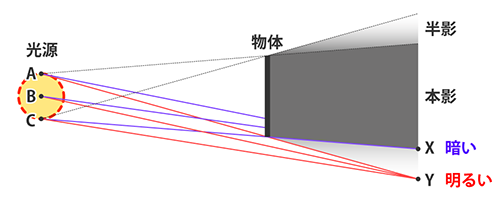
単純にモデル化したものが上図です。簡単のため、大きさを持った光源を3つの点光源A,B,Cによって表します。 点Yには3点から出発した光がすべて到達しますが、点Xに届くのはCによる光のみです。 よってYは明るく、Xは暗くなりますが、XとYの間についてはXに近づくほど光量が低下するため、結果としてぼけが発生します。 Xより内側は全ての光が届きませんので、安定して暗くなります。ここを本影(ほんえい)といいます。 XとYの間は部分的に光が届くため、中途半端に暗くなります。ここを半影(はんえい)とよびます。
大きさをもった光源については基本的にぼけが発生しますが、太陽光は比較的明瞭なエッジを作ります。なぜなら地球から見た太陽は意外と小さく、0.5°程度の視直径しかないからです。 これに対し、屋内の人工灯は太陽光よりもぼける傾向にあります。(照明器具と物体の関係次第ではありますが)
次に反射光について考えます。光は物体の表面で反射します。私たちが物を見ることができるのも、物体からの反射光が目に飛び込むためです。 この反射光の働きにより、影のエリアは周囲より暗くなる程度で済みます。仮に反射光がなければ完全な真っ黒になります。 しかし反射光を真面目に考慮し出すと、透視図法の範疇では処理しきれなくなるため、作図上、物体に当たった光は(カメラに向かう分は別にして)それ以上は反射しないものとして扱います。
この他にも光の進む距離に応じて、光量が減衰する現象などがあります。
その他のパターン
上のスライドで示す作図手順を使えば、任意の点に対する影の位置を正確に求めることができますが、カバーしきれていないパターンもあります。
まず地面以外の平面に投影する場合について考えます。元々、地面というのは生活上の感覚で使っている用語にすぎず、 任意の面を地面として扱えば、どのような平面に投影する場合も同じ手順で作図できます。 説明を簡略化するため、以降の考察では地面に投影することのみを対象とします。
次に物体が光源よりも高い位置にある場合を考えてみましょう。 投影の原理上、地面に投影される影は光源より低いものに限られます。 よって光源より高い位置にある物体は、影の描写に限定すれば存在を無視することができます。
また光源と同じ高さのものは無限遠点に投影されます。透視図上では消失点です。 実際には光は減衰するため、無限に長い影というのはありえず、消失点に向かいつつも適当な長さでフェードアウトさせることになるでしょう。