円
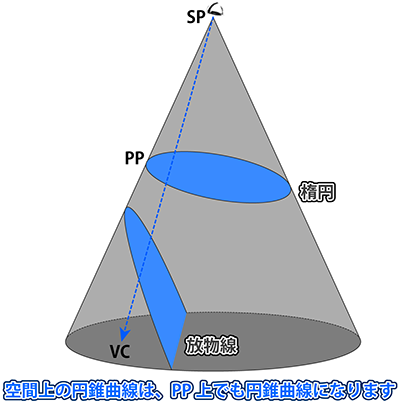
円は透視図上では、円、楕円、放物線、双曲線、直線のいずれかになります。
| 図形 | 条件 |
|---|---|
| 円 | 円が、観測者に対して正面を向いているとき |
| 楕円 | 円が、SPを通りPPと平行な平面と交点を持たないとき |
| 放物線 | 円が、SPを通りPPと平行な平面に接しているとき |
| 双曲線 | 円が、SPを通りPPと平行な平面と交差するとき |
| 直線 | 円全体が、SPを通る任意の平面上に含まれるとき |
斜円錐の断面
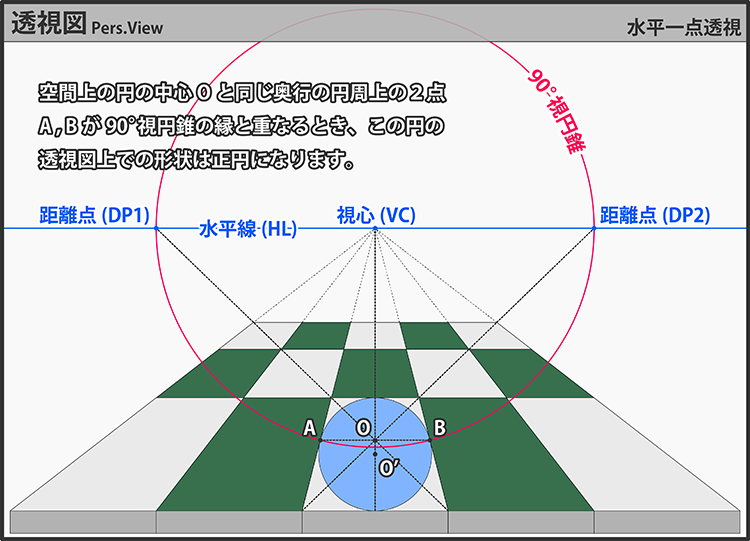
スライドP6の補足です。観測者と正対していない円が正円に見える条件は意外と複雑です。 なんとなく「円の中心Oが90°視円錐上にあるとき」と思いがちですが、そうではなく「円の中心Oと同じ奥行にある円周上の2点A,Bが90°視円錐上にあるとき」が正解です。
この法則は円の大きさに関係なく成り立ちますが、円の一部が観測者の後方に回り込む場合は、2点AB間の長さが90°視円錐の直径以上となるため、この条件を満たすことは絶対にありません。
円の属する平面としては、いわゆる地面に限定される話ではなく、任意の平面に対して成り立ちます。 円の属する平面が視心(視円錐の中心軸)と平行でない場合も、その平面の0°消失点を中心とし、同45°消失点までを半径とする円を90°視円錐相当とみなせば、同様の法則が成り立ちます。
※この証明は数学の章で解説しています。
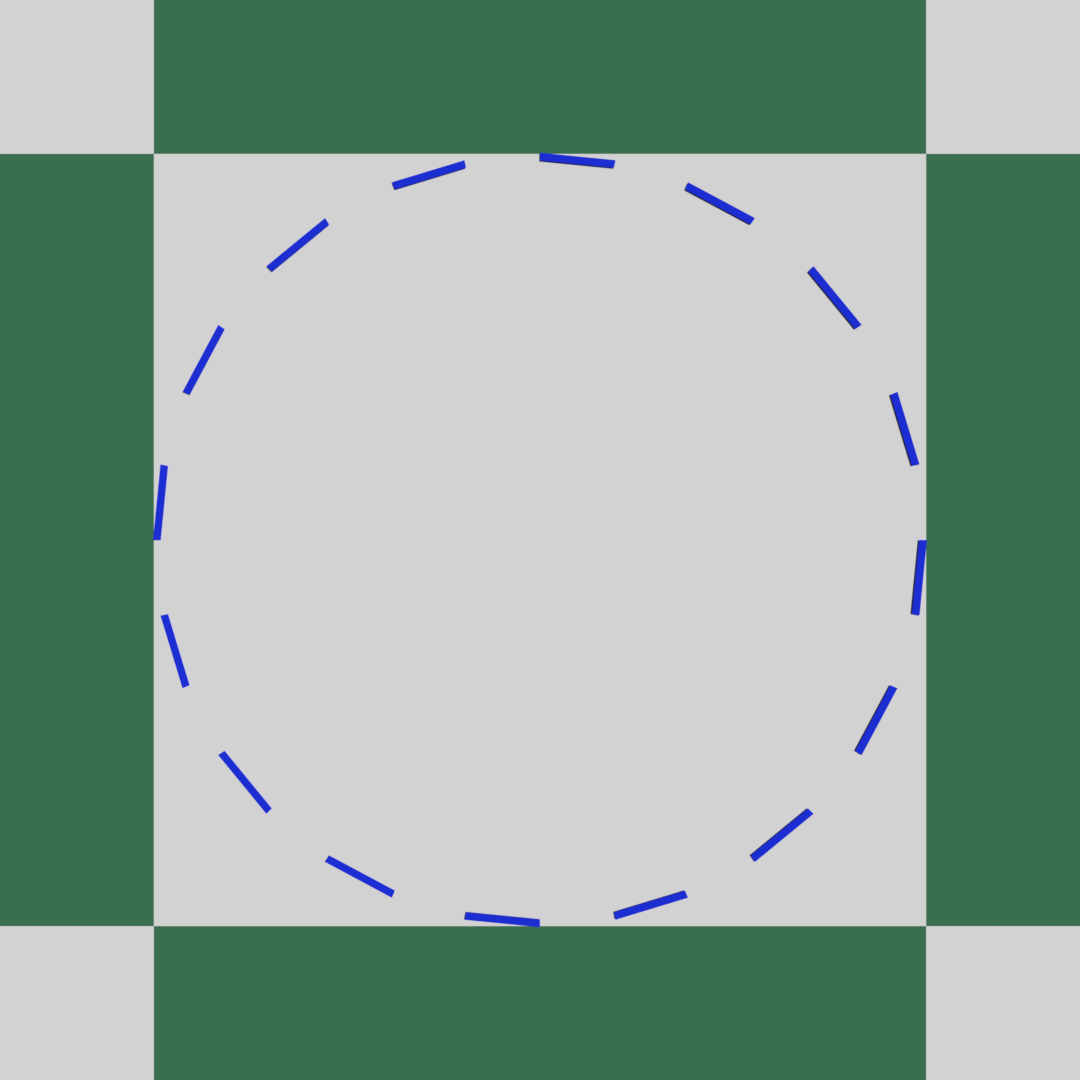
通常、円が正円に見える条件は、円を正面から見た場合に限ります。地面に描かれた円であれば、真上から見下ろした場合、すなわち俯瞰一点透視に限り正円に見えます。 ところが円を正面以外から見た場合であっても、上記コラムに示す特殊な条件を満たせば、やはり正円に見えます。
どちらも正円に見えるという点では同じですが、両者には大きな違いがあります。円を正面から見た場合はパースによる変形が一切起こらず、円およびその内外にある図形は平面図と同じ見え方になります。 ところが、円を正面以外から見つつ特殊な条件を満たした場合は、円の輪郭が見かけ上「正円」に見えるだけであり、円の内外および円周にはパースの影響を受けた変形が発生します。
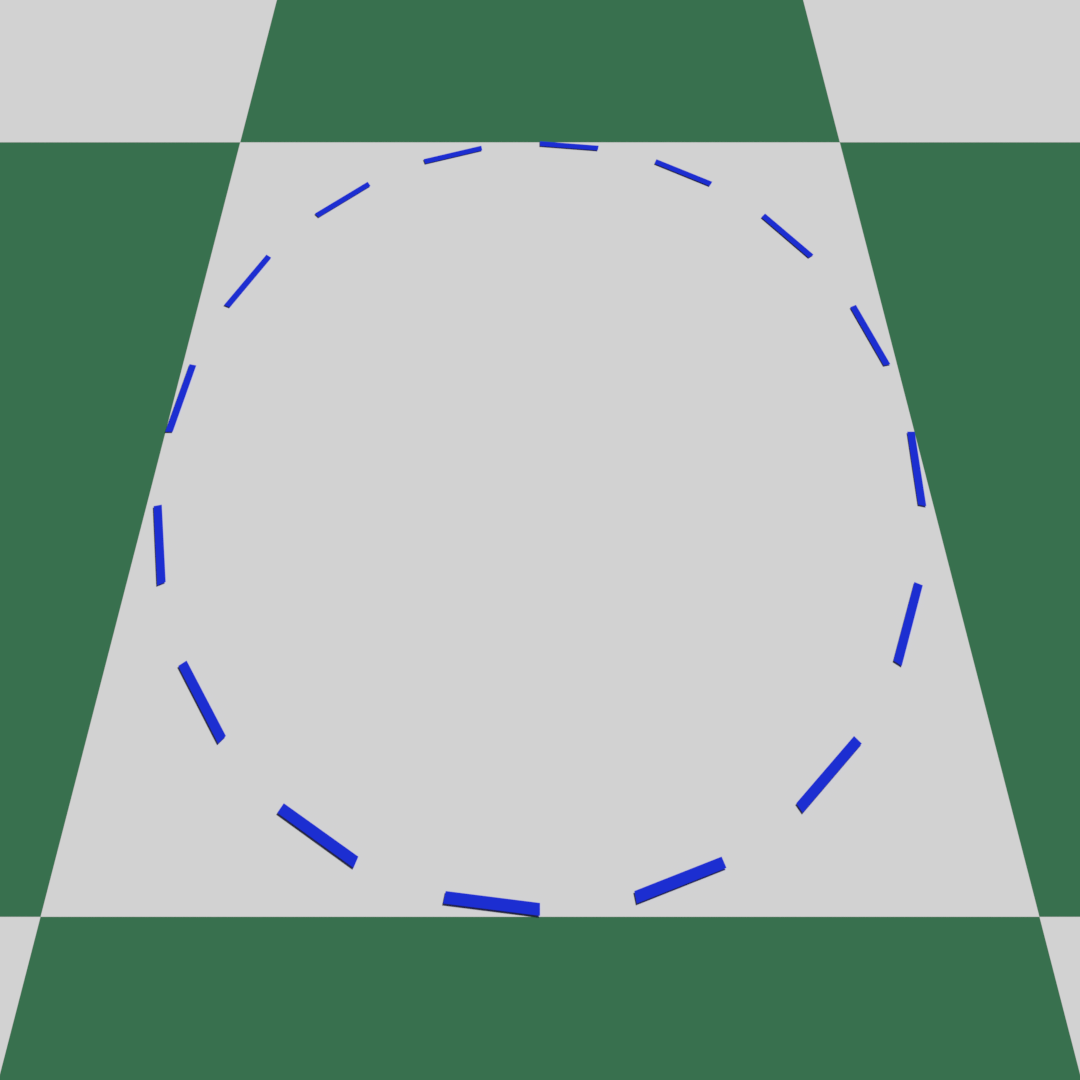
単色の円であれば、俯瞰一点透視と見分けがつかない完全な正円に見えますが、破線の場合は円の手前と奥で破線のピッチが異なるため、俯瞰一点透視と同じ見た目にはなりません。
図形の判別
傾斜面に対して同じ法則が成り立つ理由をより厳密に説明するには、足線法の作図を絡めた解説が必要となるため、別ページでの解説を予定しています。
楕円、放物線、双曲線
円錐曲線(楕円、放物線、双曲線)は円と同じく、透視図上では円、楕円、放物線、双曲線、直線のいずれかになります。
直線になる例外ケースを除けば、ある円錐曲線は自身と同じ種類かあるいは異なる種類の円錐曲線になります。
投影対象となる円錐曲線がPPと平行な平面に含まれている場合は投影後も形状が変化しません。しかしそうでない場合は形状が変化し場合によっては異なる種類の円錐曲線になります。
下図は、空間上にある放物線がPP上で楕円として投影される例を示しています。