増殖と分割
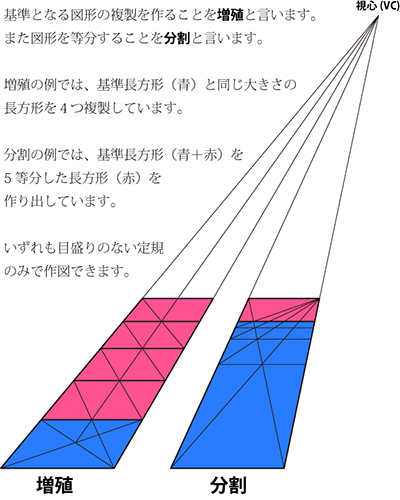
2分割
まずは2分割の例を示します。透視図と平面図の両方を載せますので、比べながら見てください。
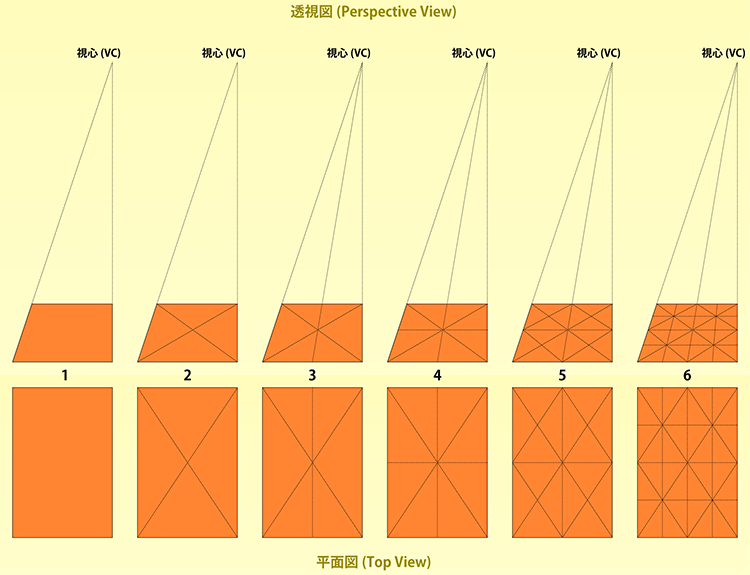
- 1個の長方形があります。この長方形を分割します。
- 対角線を引きます。
- 対角線の交点を通る直線を視心方向に伸ばします。
- 対角線の交点を通り、水平線と平行(上下の辺と平行)な直線を引きます。これで縦横それぞれの2分割が完了しました。
- さらに繰り返すと4分割もできます。図のように対角線を交差させます。
- 対角線の交点同士を縦横に結びます。今回は視心まで線を伸ばす必要はありません。4分割完了です。
n分割
次に2以上の任意の自然数nで分割する方法を示します。ここで示すのは5分割の例ですが、同じ手順で何分割でも実現できます。
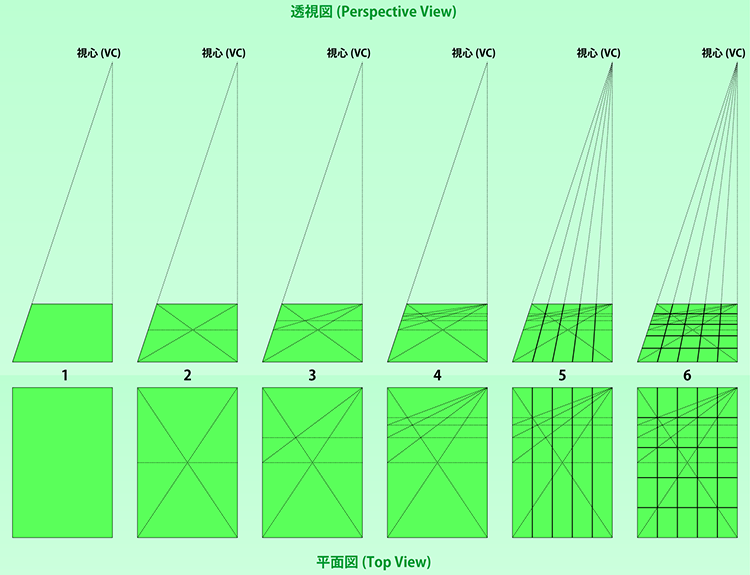
- 1個の長方形があります。この長方形を分割します。
- 対角線を引き、その交点を通る水平線(*)を引きます。ここまでで2分割です。
- 図に示す斜め線を引き、新たに発生した交点を通る水平線を引きます。ここまでで3分割です。
- 同様の手順を2回繰り返します。ここまでで4~5分割です。
- 最後に引いた水平線と右上の頂点を始点とする各斜め線との交点を通る直線を、視心から伸ばして引きます。
- 先ほど引いた5分割線と最初に引いた斜め対角線との交点の位置で、水平線を引きます。5x5のマスが完成しました。
増殖
同じ大きさの長方形を連続して並べる方法を説明します。
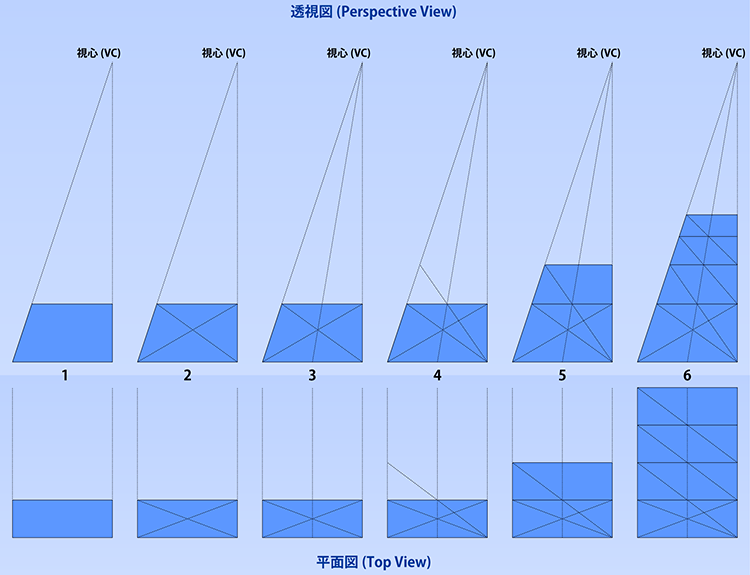
- 1個の長方形があります。この長方形を奥行方向に増殖させます。
- 対角線を引きます。
- 対角線の交点を通る直線を視心方向に伸ばします。その際に発生する長方形の辺との交点は、辺の中点になります。
- 手前の辺の端を始点とし、奥の辺の中点を通る直線を引きます。
- 新たに発生した交点を通る水平線を引きます。これで1個目の増殖が完了しました。
- 以下、同じ手順を繰り返せば、何個でも増殖できます。
増殖(枕木パターン)
線路の枕木のように、一定間隔で配置されており、かつ自身も等幅である場合の増殖方法です。
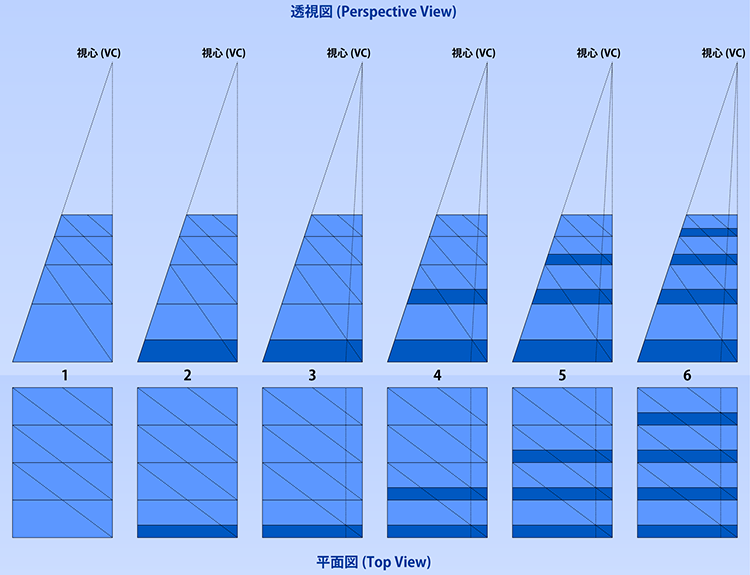
- 通常の増殖を行います。増殖に使った斜めの線は残しておきます。
- 最初のパターンの幅を決めます。任意の幅で水平線を引きます。
- 先ほど引いた水平線と斜め線の交点を通る線を視心方向に伸ばします。
- 新たに発生した交点を利用して、2個目のパターンに対する水平線を引きます。
- 同じく3個目のパターンに対する水平線を引きます。
- 同じく4個目のパターンに対する水平線を引きます。以下、必要な回数だけ繰り返します。
1点透視における分割法
1点透視における増殖法
スライドPAGE14の補足です。作図しやすい長さとは、1目盛りを1cmや5mm等の計算しやすい値にするという意味です。 この作図方は消失点の位置を先に決めることもできますが、その場合1目盛りの長さが中途半端な数字になってしまう可能性が高いです。 例えば1目盛りが1.75mmになったとすると、これを5分割する際に、1.75, 3.5, 5.25, 7.0, 8.75 という数字を計算する手間がかかり、また目盛りを読み間違えるリスクもあります。あるいは1目盛り取るたびに定規をずらす方法を取ると、意外と手間がかかるほか、累積誤差の問題があります。 よって、先に基線上に長さを取った方が速く作図できます。
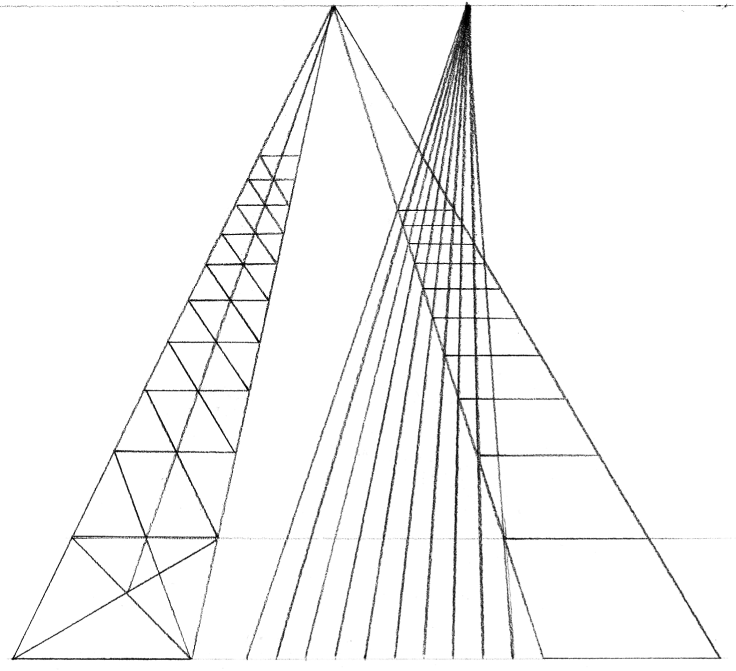
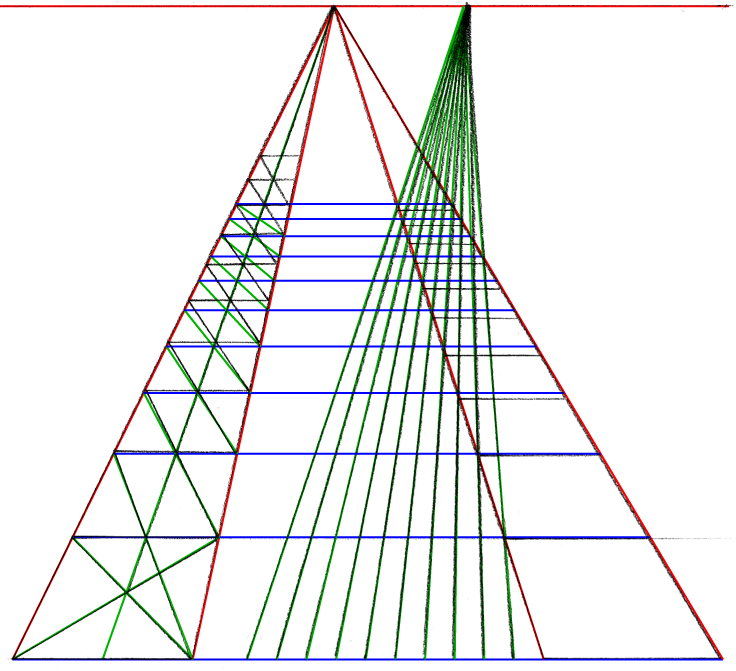
増殖方法の違いによる精度差を検証してみました。決して作為的に作ったものではなく、誰が描いても同じ傾向になると思います。 各画像の左側は追加消失点を使わない増殖、右は使う増殖です。 デジタルでは、どちらの作図法でも同じ結果になります。
アナログの場合は、右の方が精度的に有利です。
ただし最初の消失点を取る位置がずれると、すべての奥行が根こそぎ全部ずれてしまうので注意が必要です。この例では上から下までを直線で結んでいますが、実際には交点になる部分に印をつけるだけで構いません。
| アナログ | アナログ+デジタル |
|---|---|
 |
 |
絵によって精度が問題になる場合とならない場合がありますので、なにがなんでも右の方法をお勧めするわけではありません。 また精度の高いグリッドを描きたい場合は、小さい立方体を増殖するより、大きい立方体を分割した方が良いと思います。
増殖の作図例(追加消失点を使用)


