奥行の短縮率
透視図上で奥行方向に延びる直線の短縮率を調べるため、カメラの真下を始点に同じ大きさのパネルを敷き詰めることを考えます。
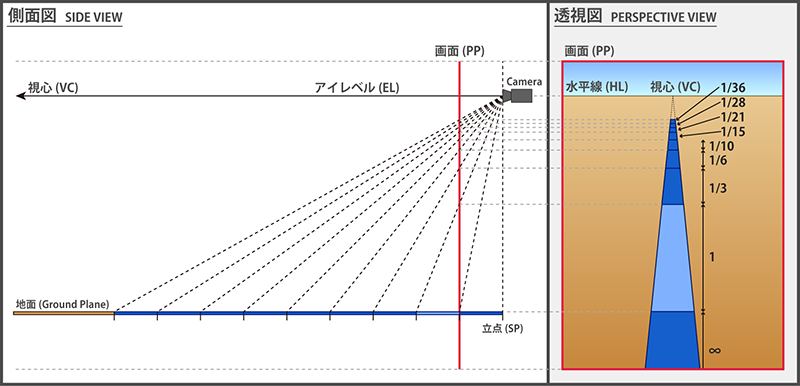
カメラの真下はPPを無限に拡大しても投影されることはありませんので、最も手前のパネルは透視図上で無限大の長さを持つことが分かります。 そこで以降は2枚目のパネル(色の薄いパネル)を基準として考えることにします。この基準パネルの透視図上での奥行方向の長さを1とし、以降のパネルがどのような長さになるかを考えたいと思います。 なお2枚目と表記しましたが、今後はこれを1枚目と呼ぶことにします。
1枚目のパネルの奥行をd1、n枚目をdnと置くと、上図の通り、d2=1/3、d3=1/6、d4=1/10……となります。 ここで分母の値は初項1、公差1の等差数列の和となりますが、それを証明するためdnがどのように書き下せるかを考えます。
1枚目のパネルの幅は1と置きましたので、地面からカメラまでの高さは2に相当します。
(1点透視―奥行の短縮率のスライドも参照してください)
n枚目のパネルの幅は全体幅2から、n-1枚目までの幅を差し引いた後、n+1で除算した値と一致しますので、
以下の通りとなります。

得られた結果は、初項1、公差1の等差数列の和の逆数となっていることが確認できます。
概要 ― 遠近感の節では、奥行方向の長さがカメラからの距離の2乗に概ね反比例することを述べましたが、ここでその証明を行います。
n枚目のパネル長はdnですが、このパネルの手前の辺に対してa倍の距離を取ると、そこにあるパネルはan枚目となります。2つのパネル長の比を計算すると、
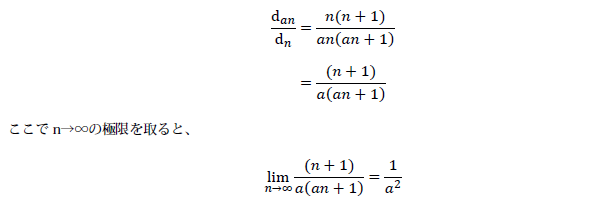
となり、カメラから遠ざかるにつれて、奥行方向の長さはカメラからの距離の2乗に反比例することが分かります。
「概ね(おおむね)」という断りを付けた理由も、上式を見ればお分かり頂けるかと思います。
距離の2乗に反比例という法則は近似であり厳密には成り立ちません。
とはいえ極端に長い物体でない限りは、(適正画角内では)ほぼ成り立つと考えてもらって問題ありません。


