消失線とSP - 応用 - パースフリークス

はじめに

この節では消失線の分類および、各消失線に対応するSPの取り方について説明します。透視図法における平面は、大別すると下表の３種類に分類されます。このうち消失線を持つ平面は、下２つのいずれかとなります。

平面の分類	消失線	解説
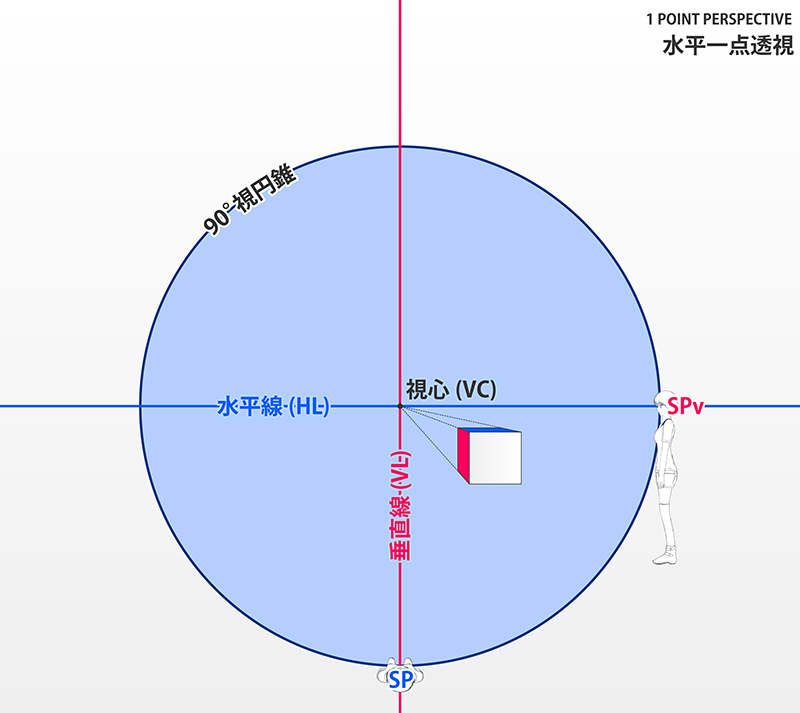
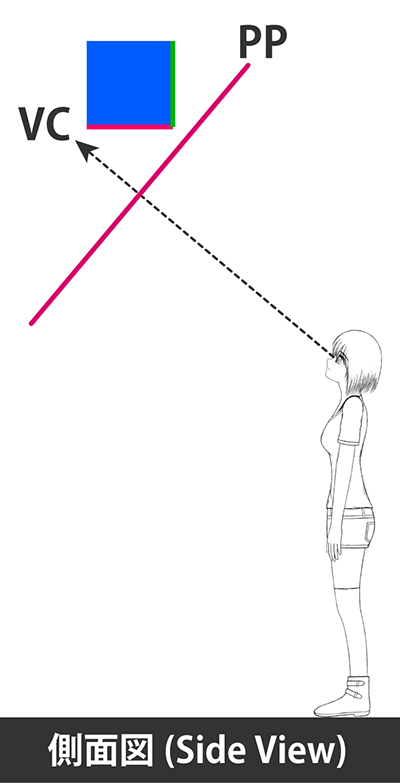
PPと平行	持たない	PPと平行な平面とは、カメラと正対している平面、すなわちカメラから同一距離(*)にある点の集合が作る平面のことです。この平面は消失線を持たず、平面上のあらゆる直線も消失点を持ちません。１点透視図の１つの面がこれに該当します。
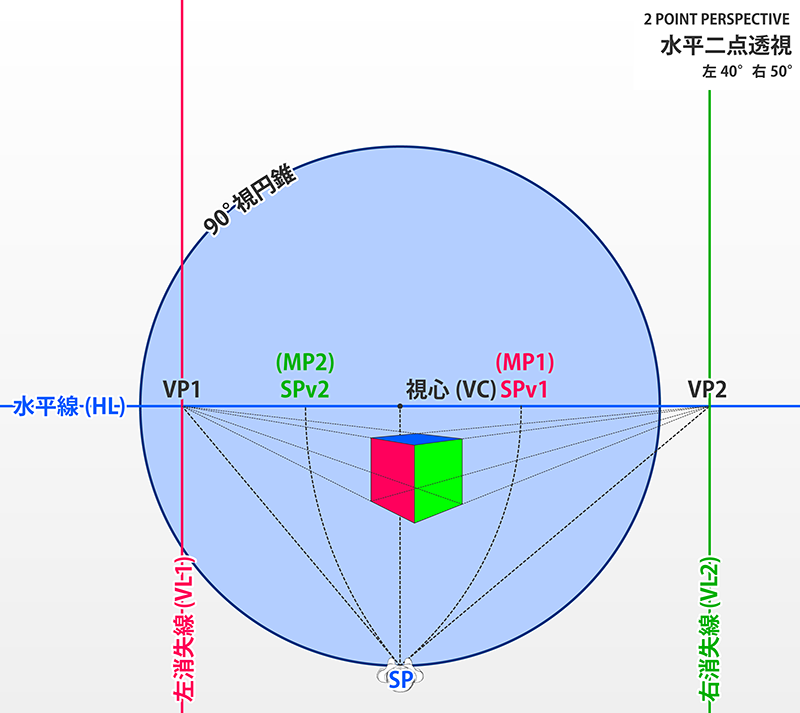
PPと垂直	持つ (視心を通る)	PPと垂直な平面は、消失線が視心を通るという特徴を持ちます。対応するSPは90°視円錐の縁に現れます。図法的には扱いやすいと言えます。１点透視図の２つの面、および２点透視図の１つの面がこれに該当します。
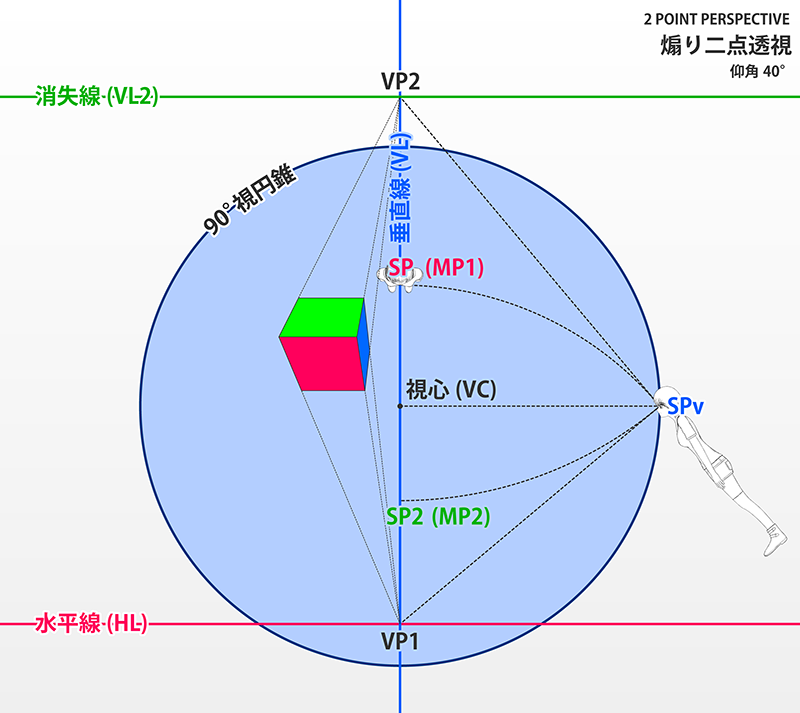
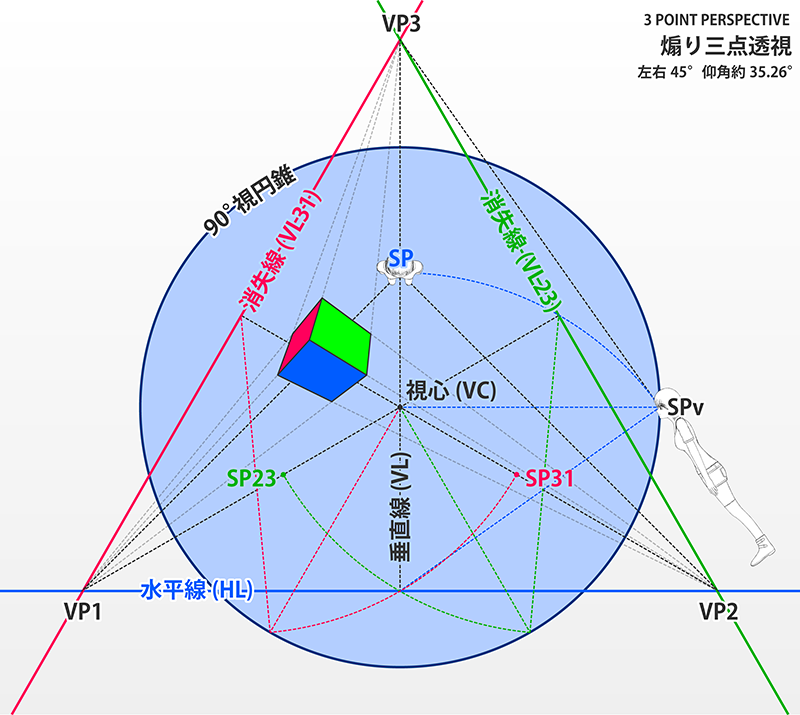
PPと斜め交差 (平行でも垂直でもない)	持つ (視心を通らない)	PPと平行でも垂直でもない平面は、消失線が視心を通りません。対応するSPは90°視円錐の内側に現れます。図法的な難度は高めです。２点透視図の２つの面、および３点透視図のすべての面がこれに該当します。

※透視図法における距離の考え方については、概要の章を参照してください。

１点、２点および３点透視図における消失線とそれに対応するSPを下表に示します。

平面の分類	透視図	解説
白：PPと平行青：PPと垂直赤：PPと垂直		１点透視図は正対面を除く２つの平面が消失線を持ちます。２つの平面はPPと直交しているため、２本の消失線は視心を通ります。また２本の消失線は直交します。
青：PPと垂直赤：PPと斜め緑：PPと斜め		２点透視図は１つの面（青い面）がPPと直交しているため、消失線が視心を通ります。残り２つの面はPPと斜めで交差するため、消失線が視心を通りません。この２面に対応するSPは測点と同じ位置に発生します。３本の消失線は互いに平行または直交します。
青：PPと垂直赤：PPと斜め緑：PPと斜め		垂直２点透視図は、図の構造的には水平２点透視図とまったく同じです。ただし空間的な意味を考えると、赤線が水平線であるのに対し、緑線の意味合いを掴みづらいかもしれません。赤は地面と平行な平面であり、青と緑は共に地面と垂直な平面です。青はPPとも直交していますが、緑は直交していません。
青：PPと斜め赤：PPと斜め緑：PPと斜め		３点透視図は３つの面すべてがPPと斜め交差します。よって３本の消失線はいずれもが視心を通りません。また３本の消失線は互いに平行にも垂直にもならず、三角形を描きます。

消失線は図法的に分類すると、視心を通るか否かの２種類しかありません。つまり覚えるべき作図法は２パターンに限定されます。特に平面図形（円など）に関しては、平面間に相似性があるため、同一の作図法をあらゆる平面に適用できます。

次のスライドでは消失線の図法的分類の解説を交えながら、消失線に対するSPの取り方について説明します。SPを取る理由は主に３つぐらいあります。

PAGE 1/x

消失線の分類とSPの取り方

以下の手順はスライドP12を参照してください。

視心から消失線に向かって下した垂線の足が0°消失点になります。
視心から消失線と平行な直線を引き、90°視円錐との交点を求めます。
0°消失点と手順２で求めた点を直線で結びます。
0°消失点を中心とし、３を半径とする円を描き、直線１の延長上で交点を求めると、そこがSPになります。（平面図SPと区別するため、SPsと表記することにします。sはslopeのsですが本サイトでしか通用しない表記です）

※作図原理は画角の立体的解釈のスライド後半を参照してください。

SPを作図するには90°視円錐が必要です。正確には90°視円錐の半径が必要です。実際に円を作図していなくても、半径の値さえ把握できていれば、物差し１本でも作図できます。

制約のない画面であれば半径を自由に決めることができます。また制約がある場合でも１、２点透視図であれば半径を求めるのは簡単です。１点透視図は視心から距離点までの長さが90°視円錐の半径になります。２点透視図の場合は、視心から２つの消失点までの長さa,bを測れば、90°視円錐の半径は√abで求めることができます。

amazon co.jp アソシエイト