遠くのものほど小さく映る
※以下に「カメラ」とありますが、「観測者」と同じ意味です。
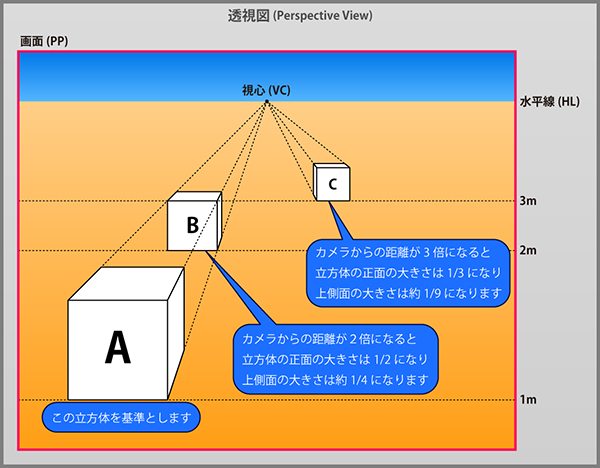
実空間上で同じ大きさのものであっても、透視図法で表現すると、カメラから遠ざかるにつれて小さく描写されます。
縮小率は図に示す通り、カメラからの距離に反比例します。すなわちカメラからの距離が2倍になれば、
画面上での大きさは半分になり、3倍になれば1/3になります。ただし、奥行方向の面に関しては概ね距離の2乗に反比例します。
すなわち、カメラからの距離が2倍になれば、画面上での大きさは約1/4になり、3倍になれば約1/9になります。
(大きさは面積比ではなく長さの比です)
ここで透視図法における距離の考え方を説明しておきます。
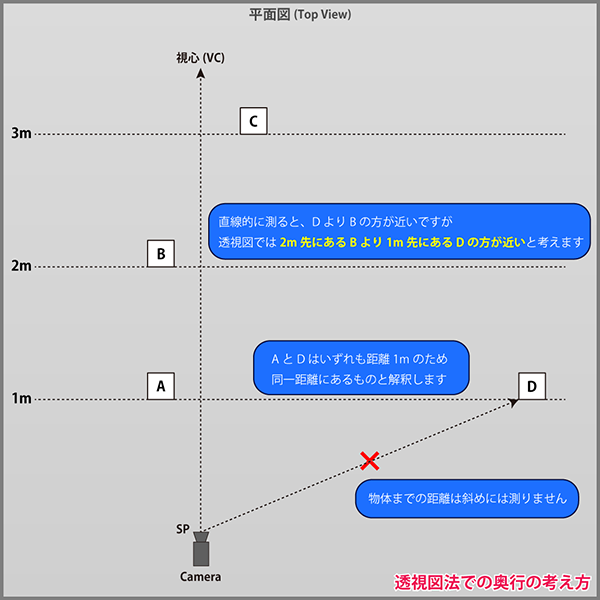
通常、2点間の距離は単純に直線を引いて考えますが、透視図法では視線の向きに直交する面を考え、
面上に存在するすべての点は、カメラから面までの最短距離を以って、その点までの距離とみなします。
すなわち下図のように、距離1mの面上にあるすべての物体は、たとえ直線距離が10mあろうと、100mあろうと、
「カメラからの距離は1mである」とみなすのです。
下図の例ではAとDはいずれもカメラからの距離は1mです。Bは2m、Cは3mになります。
しかし、なぜこのような考え方をするのかという疑問が生じます。
透視図法は遠近法であり、遠くのものほど小さく描画されますが、逆に言えば、元々同じ大きさの物体が透視図上でも同じ大きさで投影されるのであれば、それらの物体はカメラから同一距離にある、と考えることができそうです。
そこで前述の考えに基づき、カメラから同じ距離の位置に複数の物体を並べ、それぞれの透視図上での大きさを調べてみることにします。
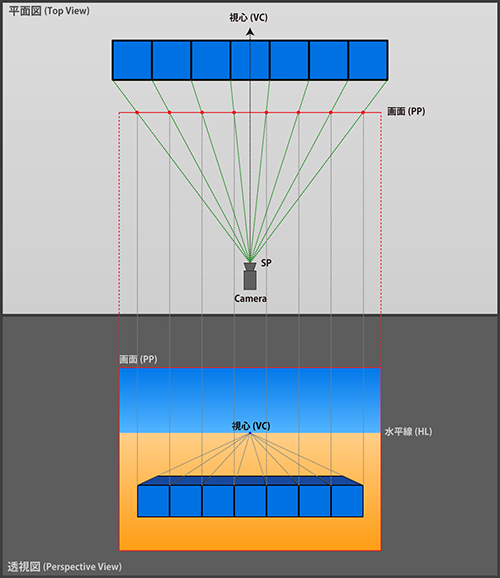
上図の例では、カメラから等距離の位置に立方体を並べています。
これらの立方体の頂点とSPを結ぶ足線(視線)がPPと交差する位置を調べてみると、その間隔が等しいことが分かります。
交点の間隔が等しいということは、すべての立方体が透視図上で同じ大きさに投影されることを意味します。
すなわち、上記の仮説は正しかったことになります。
物体の大きさは距離に反比例する
ここでは同じ大きさの物体を複数並べたときに、透視図上での見かけの大きさがカメラからの距離に反比例することを図解します。

