消失点はなぜ発生するか?
正方形のパネルを地面に貼り付けたときの見え方を考えます。
パネルを奥の方に伸ばしていくと、消失点(Vanishing Point, 略記VP)と呼ばれる点に収束するのが分かります。
透視図法ではこの法則を利用して作図を行うのが主なわけですが、
そもそもなぜこのような法則が発生するのでしょうか?
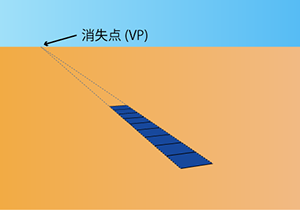
消失点の発生原理(水平方向)
PAGE 1/x
消失点の発生原理(水平方向)
消失点の発生位置(水平方向)
消失点の位置は、投影しようとしている直線の角度に依存しますが、もう少し掘り下げて考えてみたいと思います。
PAGE 1/x
消失点の発生位置(水平方向)
[Click] 消失点を持たないとは?
消失点は、観測者から見て無限の彼方にある点を指します。数学では、これを無限遠点と呼びます。 無限遠点は無限の彼方にあるわけですから本来であれば見えないはずですが、透視図上では視認可能な点として現れます。 (消失点は画面の外に出ることもありますが、画面を拡張すれば出現します)。
ところが例外があり、観測者から同一距離にある点の集合、すなわちPPと平行な直線は消失点を持ちません。 消失点を持たないということは、透視図上であっても無限遠点に相当する点が見える点として現れないということです。 すなわち画面をどれだけ拡張しても、その直線は無限にどこまでも伸びていきます。
以上をまとめると、消失点を持つ直線は透視図上では半直線となり、消失点を持たない直線は透視図上でも直線になります。
消失点の発生原理(水平方向)まとめ
消失点の位置は角度に依存します。投影対象の直線と平行な直線をSPから伸ばし、PPと交差する位置に消失点が発生します。 これを踏まえると、以下の法則が成り立ちます。
- 実空間上で平行な直線は、透視図上では同一の消失点に収束します。
- 実空間上で平行でない直線は、透視図上では別々の消失点に収束します。
- PPと平行な直線は、消失点を持ちません。


スポンサーリンク
amazon co.jp アソシエイト
