寸法の測り方
この節では1点透視図における寸法の測り方を説明します。主な方法として次の3種が挙げられます。
| 基準 | 要点と特徴 |
|---|---|
| 物体 | 基準となる物体を画面内に配置しているときに使用可能な方法です。基準物体から平行線を引くことで、長さを取得します。基準物体が同一の奥行に存在する場合は、平行移動または回転を利用します。 |
| アイレベル | アイレベルを長さの基準とする方法です。直感的で分かりやすいため、後述する画角を使用する方法よりも、こちらを優先して使うことをお勧めします。 |
| 画角 (90°視円錐) | 画角または90°視円錐を使って長さを求める方法です。アイレベル基準の方法ほどお手軽ではありませんが、アイレベルを規定できない空間であっても通用するため、より汎用的な方法であると言えます。 |
他の物体の長さを参照する
上のスライドでは説明していませんが、奥行方向の辺を平行移動させる別の方法を紹介しておきます。
まず距離点(*)を使って一旦水平線と平行な向きまで回転させ、そのあと別の奥行に平行移動させます。そこで再度距離点を使用して奥行方向の辺に戻します。
このやり方だと、水平方向に変換した際に長さを調節できるので、より汎用性が高いと言えます。
*:距離点を使うのが無難ではありますが、水平線上の他の消失点を使っても同じ結果を得ることができます。
上のスライドでは1/2および1/4の距離点の例しか示していませんが、どのような比率であっても、同じように作図することができます。
しかしアナログでの作画に限れば、1/2(中点)や1/4(中点の中点)を使うことをお勧めします。
1/3や1/5などの半端な長さは電卓が必要な場合もあり、測るのに時間がかかるからです。
消失点については1枚の絵について1回取るだけで済みますが、物体側の内分点は物体の数だけ取らなければならないことに注意してください。
※このタイプの定規であれば、中点がすばやく取れます。

上で示す方法は画面上に寸法が既知の物体を配置している場合にのみ使えます。 このような言い方をすると、まずはリファレンスとなる何かを配置する必要があるのかと思うかもしれませんが、 むしろ逆で、画面上に何かを置いてしまうと、以降に配置するものは配置済の物体に合わせた描き方をしなければならなくなります。 つまり画面上の他の物体は長さを測る便利な物差しであると同時に、描き手を縛る拘束具でもあるということです。 本サイトではこれを「制約」と呼んでいます。
背景の作画が難しい理由の1つに、画面が多くの制約に縛られることが挙げられます。 画面が真っ白な状態は、視点、アイレベル、寸法などがすべて未定であると言えます。 この状態で物を置くのは簡単で、自分の最も得意とする構図で作画することができます。 しかし、一旦制約が生まれると、作画の自由度は激減します。 自由度のない状態で如何に他オブジェクトとの整合性を取るかは常に重要な課題であり、パース理論を学ぶ最大の理由でもあると言えるでしょう。
アイレベルから長さを取得する
水平方向の1点透視図および2点透視図ではアイレベルを長さの基準として使うことができます。 次のスライドではアイレベルを物差し代わりにして、物体の長さを測る方法について説明します。
アイレベルを明確に定めないまま物体を画面に配置した場合は、物体からアイレベルを逆算することができます。 やり方は簡単で、物体の長さを基準に地面からアイレベルまでの高さを測れば良いだけです。
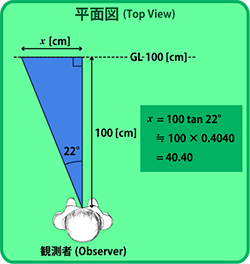
画角または90°視円錐を使って、長さを取得する
アイレベルが不明なときや、アイレベルを規定しづらい空間(宇宙空間や垂直1点透視など)では、アイレベル基準の寸法測量ができません。 そこで次のスライドでは画角または90°視円錐を使った長さの測り方を説明します。
GLとELの関係について補足しておきます。上のスライドでは最初に1m先の地面(GL)を適当な位置に設定していますが、これはアイレベルが未定だからこそ可能な技です。ある奥行におけるGLの位置を決めると、その瞬間にアイレベルが決定し、以降はELもGLも自由に設定することはできなくなります。また逆にELの高さが確定している画面内では(距離が明確に指定された)GLを自由な位置に取ることはできません。
さらに複雑な話をすると、視心と水平線の位置のみを定め、90°視円錐の半径(SPの位置)が定まっていない画面を用意したとします。 この場合は、ある奥行におけるGLを指定した上で、なおかつELも任意の高さに指定することができます。両者を指定した瞬間に90°視円錐の半径が自動決定します。
つまりSP,GL,ELは2つを決定すると、残り1つが確定する関係下にあると言えます。
奥行の短縮率
次のスライドでは、物体と水平線との間にできる隙間を測ることで、カメラ視点(SP)を割り出す方法を示します。かなり応用的な技になりますが、この方法を覚えておけば、物体の奥行幅をより直感的に決定できます。