パース円の性質(楕円の中心)
上のスライドで示す作図手順が成立する理由については、数学の章で解説しています。
円に外接する正方形は1つではなく、様々な向きに描くことができます。 外接正方形の見かけの形状が台形でない場合であっても、正方形を回転させれば台形となる向きが必ず存在します。 このとき元の図形が2点透視であれば1点透視に、3点透視であれば2点透視に変化します。 よってパースで円を描くときは、1点透視と2点透視の2パターンのみを考慮すれば良いことになります。
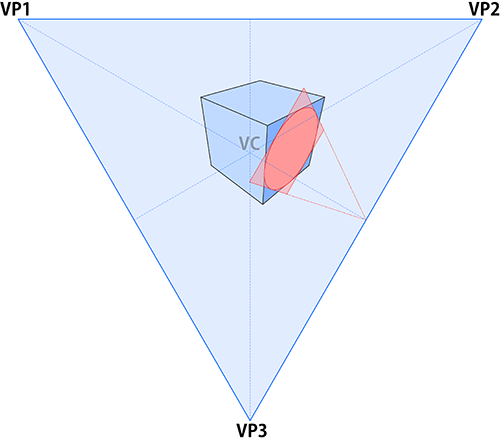
下図では3点透視図の立方体の1つの面に内接する円を描こうとしています。この場合、正方形の1対の辺が消失線と平行になるまで回転させれば、正方形の見かけの形状は台形に変化します。
一旦台形になってしまえば、上のスライドで示す性質を利用して作図できます。ここで描かれた円は回転前と回転後のいずれの正方形に対しても内接していることに注意してください。
パース円の性質(楕円の軸)
ここで示す性質が成り立つ理由については、非常に複雑な説明を要するため、数学の章での解説を予定しています。(現在準備中です。今しばらくお待ちください)
同心円
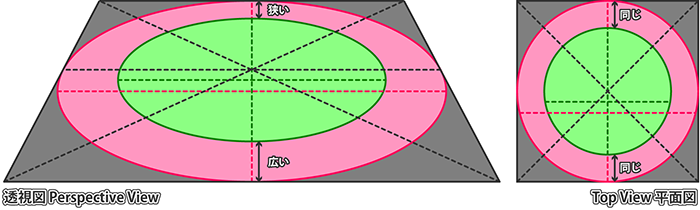
全体がカメラの前方にある同心円について考えます。 中心を共有する2つの円がカメラに対して正対していない場合、透視図上ではそれぞれの円は楕円に変形しますが、2つの楕円の中心は一致しません。
下図の赤い円と緑の円は空間上では中心を共有しています。すなわち同心円です。しかし、透視図上での2つの楕円は中心が一致しません。ここで赤いリング(赤い円から緑の円をくり抜いた部分)に注目してください。
空間上ではリングの手前と奥は同じ幅ですが、透視図上では「遠くのものほど小さくなる」法則が働くため、奥の方が幅が狭くなります。すなわち内側の楕円の中心は、外側の楕円の中心よりも、少し奥にずれることを意味します。