立方体の描き方
この節では立方体の描き方を4種ほど説明します。
| 作図法 | SP | 平面図 | 追加 消失点 | 要点と特徴 |
|---|---|---|---|---|
| 測点法 | 要 | 不要 | 要 | 基線上に実長を取り、これを立方体の各辺の向きに回転させることで、正確な長さを測ります。回転を行うには「測点」と呼ばれる追加の消失点が必要です。 |
| 介線法 | 要 | 不要 | 要 | 立方体の高さ方向の面に対して、対角線の消失点を求め、それを作図に利用する方法です。広い作図スペースを必要とするのが難点です。また高さ方向の面を描く技術なため、地面に沿った正方形を描くことには向いていません。 |
| 足線法 | 要 | 要 | 不要 | 視点(SP)と物体を結ぶ直線(足線)を引くことで、投影位置を求める作図法です。直感的で分かりやすい反面、正確に描くにはSPと物体の位置関係および寸法を正しく表現した平面図を必要とします。 |
| 基線法 | 不要 | 要 | 不要 | 基線上に任意の点を取り、対応する消失点に補助線を引くことで立方体の奥行を求めます。立方体の軸に対応する2つの消失点を使う方法が基本ですが、応用すれば任意の消失点を使って同様の作図が可能です。真上から見たときの正方形を作画の補助として使います。 |
いずれの方法も、如何にして立方体の奥行を正確に求めるかが技術的要所になります。また高さ方向の辺との整合性も確保する必要があります。 どの作図方法を使っても、得られる結果は同じですので、いずれか1つでも習得すれば、正確な立方体が描けるようになります。
立方体の描き方(測点法)
立方体の描き方(介線法)
傾斜角が45度の傾斜消失点に収束する直線のことを介線(medium line)と呼びます。
スライドに例示した直角三角形の高さ:底辺=1:2となる傾斜角の場合を、便宜上「1/2介線」と呼ぶこともあります。
参考文献:建築の新透視図法 新訂版 (長尾勝馬著) P45,57
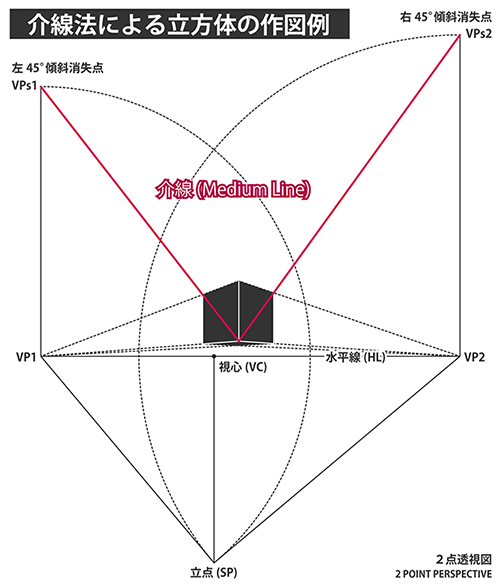
介線法はHL上にある消失点の上下に追加の消失点を取る方式なため、広大な作業スペースを必要とする傾向があります。 ここでは紹介していませんが、介線法には縮図を利用し狭い作業領域で作図を行う手法が存在します。 ただし、その方法を使うには視心(VC)やSPの位置が確定していないことが条件であり、作画の過程で視心とSPが受動的に決定します。 その代償として画角の制御が難しく、同じ手順を繰り返して2個以上の立方体を作図しづらいという欠点があります。(最初に描いた立方体を増殖することはできます)
参考文献:建築の新透視図法 新訂版 (長尾勝馬著) P54
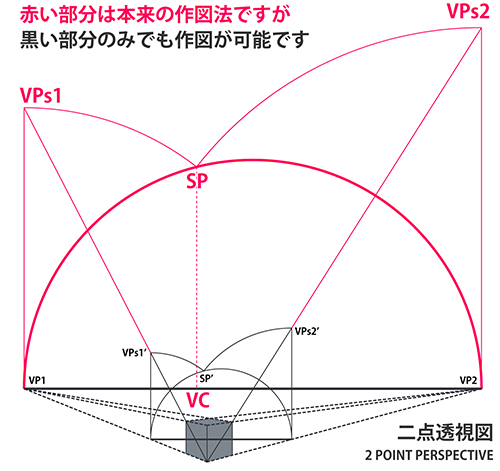
要点だけ掻い摘んで説明しておきます。 本来の作図域は赤い部分ですが、これを描かずに黒い部分のみの作図で立方体を描くことができます。 狭い紙面でも作図ができるので、上手に活用すれば非常に便利な方法と言えます。
注意してほしいのは、黒のSP'や傾斜消失点は本物ではないということです。この消失点を利用して作図できるのは、 下図の位置に描かれた立方体に限られ、他の位置に別の立方体を描く場合は、本物の傾斜消失点を使うか、 別途縮図を描かなければなりません。
要は立方体毎に専用の縮図が必要だということです。 縮図を描く場合、最初の1個に限ればSP'を適当な位置に取ることができますが、 2個目以降は1個目の縮図と相似になるようSP'の位置を合わせる必要があります。
また視心はSP'の真下に来ないので注意してください。
立方体の描き方(足線法)
上のスライドでは例示していませんが、透視図上のHLと平面図上のPPが重なるよう両図を重ねて描けば、手順と作業スペースを省力化できます。
練習すれば可能かもしれません。まず透視図上にラフで立方体を描き、それを元に逆算的に足点を求め、そこからSPと正方形の位置関係や向きを類推します。その後、通常の手順で透視図を描き、正確な立方体を完成させます。
立方体の描き方(基線法)


