はじめに
透視投影は3次元コンピュータグラフィックス(3DCG)の世界でも盛んに使われています。 現在、世の中に普及している3DCGソフトは、透視投影をメインの投影法として採用しています。 よって3DCGで描画される図は透視図法で描いた図と、理論上は完全に同じものになります。
この節では3DCG技術のうち、透視投影に関連するものを主に説明していきます。
透視図法と3DCGの違い
コンピュータは人間とは異なり、消失点を利用しません。また1点透視、2点透視、3点透視という分類も行いません。 この点において、3DCGはハードウェアであるカメラと同じ性質を持っています。 カメラはその内部機構として、1~3点透視の分類を行っていませんし、消失点も取っていません。 にも拘わらず、私たちが透視図法で描いたものと同じ像を作り出すことができます。 この理由を概念的に説明すると「カメラやコンピュータは透視図の定義による作図を力技で行っているから」に他なりません。
あの作図法は定義に沿った単純なものであり、消失点も1~3点透視の分類も必要としません。 ある意味、非常にシンプルかつ強力な方法ですが、あの手の単純な繰り返し作業は機械やコンピュータが運用してこそ力を発揮するものです。 人間が手作業でパースを解決するには、やはり消失点や1~3点透視という概念が必要と言えます。
3Dソフトはレンダリングの際に消失点を利用しませんし、ユーザーもまた消失点を意識する必要がないため、基本的に3Dソフトは指定した直線に対する消失点や、指定した平面に対する消失線を表示する機能は持っていないと考えた方が良いでしょう。 代替案として、無限の彼方まで続く直線や平面オブジェクトを配置すれば消失点や消失線を擬似的に引けるという考えがありますが、3Dソフトは物体の大きさに上限が設けられていたり、視野の奥行が限定されていることも少なくないため、必ずしも容易な選択とはならないようです。
透視図法がすぐに廃れることはないと思っています。 コンピュータの高速性と正確さは魅力ではありますが、描き手の頭の中のイメージを自動的に吸い出してくれるわけではありませんし、自発的に絵を描いてくれるわけでもありません。 ここが人間との違いです。頭の中に描きたいイメージがあり、それをどこにも伝達する必要なく、いきなり線を引くことができる。 これは絵描きだけが持っているアドバンテージです。 なにはともあれ3DCGで絵を作るなら、モデリング、シーンの構成、光源設定、そしてカメラワーク、こだわるならテクスチャマッピングと、多岐に渡る作業をこなすしかありません。 これらの作業は透視図法を使った作図よりも手間がかかることがほとんどです。
とはいえ使い回しの利くオブジェクトや、頻出する複雑な背景シーンなどを作る分には、コストの回収も見込めるでしょう。 よって1度限りのシーンは透視図法で、再利用パーツは3DCGで、のように使い分けることが有効だと思います。
3DCGとは
3DCG(three dimensional computer graphics)とは3次元コンピュータグラフィックスの略であり、与えられた3次元データをもとに2次元の画像を作り出すこと、あるいはそのような手法で作られた画像を指す言葉です。 もちろんCGと呼ぶからには、コンピュータの演算によって画素を形成することが絶対条件です。 よって写真のように現実世界の光を利用して作成されたものはCGではありません。 またペイントソフトを使って人の手で直接描かれたものも、3次元データを介していないので(いかに立体的に見えても)3DCGとは呼ばれません。
Cyclesレンダリングエンジン(Blender)による作例:学校の教室


上の画像は3DCGの例です。3DCGのメリットは、同一のシーンを様々な視点から描写できることです。
コンピュータは物体を描画する際に、透視図の定義に基づき頂点の投影位置を計算で直接算出します。 通常3つないし4つの頂点を集めて面を形成します。 このときできる三角形や四角形をポリゴンと呼びます。
どのような複雑な物体でも三角形や四角形の集まりで表現できますので、3DCGのレンダリング(2Dの画像を描き出すこと)は、ポリゴンの描画に帰着します。 (ポリゴン以外に自由曲線を扱える場合もありますが、やはりポリゴンが主役です)
なお、実際のレンダリングでは面に質感(テクスチャ)や陰影(シェーディング)を付ける必要がありますが、 パース理論から脱線しますので、本サイトでは扱いません。 付影処理(シャドーイング)については陰影の章を参照してください。3DCG的な解説ではありませんが、原理としては同じものです。
3DCG制作ソフトの分類
3DCGの制作工程は大別するとモデリングとレンダリングに分かれます。 モデリングとレンダリングは異なるソフトが担当していることも少なくありません。 モデリング機能を持つソフトをモデラー、レンダリング機能を持つソフトをレンダラーといいます。両者の機能を合わせ持ったものも存在します。
| 工程 | 概要 |
|---|---|
| モデリング | 3Dオブジェクトの形状を作る工程。実世界において粘土をこねて物体の造形を作り出すような作業をイメージしてください。これを画面上で行うことになります。操作はペンタブレットではなく、マウスを使うのが一般的です。モデルには変形のない固定モデル(建物等)と、関節等が動く可動モデル(人間等)があります。もちろん可動モデルの方がモデリングの難易度は高くなります。 |
| レンダリング | モデリングによって作られたオブジェクトを、透視投影によって2Dの画像として描き出す工程です。前準備として、シーン内に3Dオブジェクトを配置し、光源とカメラを設定する必要があります。基本は静止画ですが、動画(アニメーション)を作る機能を持ったレンダラーもあります。 |
3D表示を行うゲームを制作する場合は、素材としてのモデリングは必要ですが、レンダリングはリアルタイムで行うことになるため、プログラミングも必要となります。 代表的なリアルタイム3DCGライブラリとしてDirectX(Direct3D)やOpenGLがあります。これらのAPIを呼び出して、専用の表示機能を作成することになります。
3DCGにおける透視投影の座標変換
3DCGで使われている投影方式は、補助的に平行投影も使われるとはいえ、基本は透視投影です。 ここでは透視投影によって、物体がどのような座標変換を経て画面に投影されるかについて考えます。
説明を簡略化するため、モデルは簡素なものを使います。 3次元空間の座標軸を小文字のxyzとし、図に示す通り左手系を使うものとします。 カメラ(SP)は原点に配置し、その向きはz軸正方向とします。すなわちz軸方向が奥行になります。画面は平面z=1に置きます。 画面には独自のローカル座標系XYを設けますが、X軸とY軸はそれぞれ小文字のx軸やy軸と平行な方向かつ座標値が同じになるよう取ってあります。 画面座標系の原点(0,0)は空間座標系の(0,0,1)と一致します。
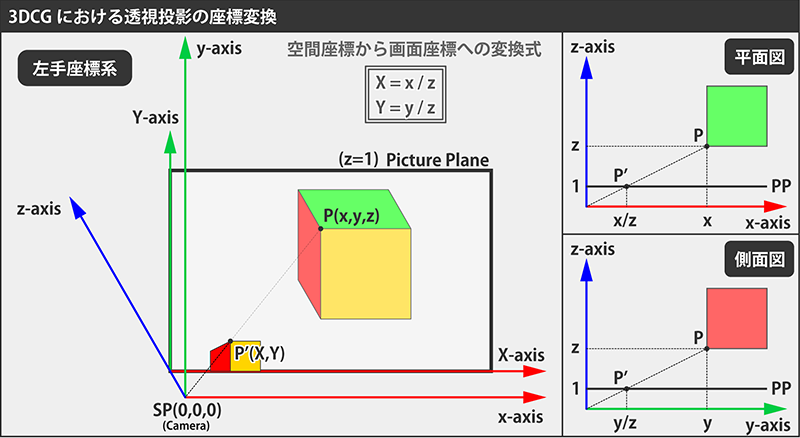
さて、舞台は整いました。3次元空間内の任意の点P(x,y,z)が画面上の座標P'(X,Y)に変換されるとき、両者の座標にどのような関係性があるかを考えます。 ここでは画角は考慮しません。しかしカメラの後方は投影できないため、z>0の条件はつけるものとします。 透視投影の座標変換式は比較的シンプルな形で表現できます。
| X=x/z |
| Y=y/z |
視錐台
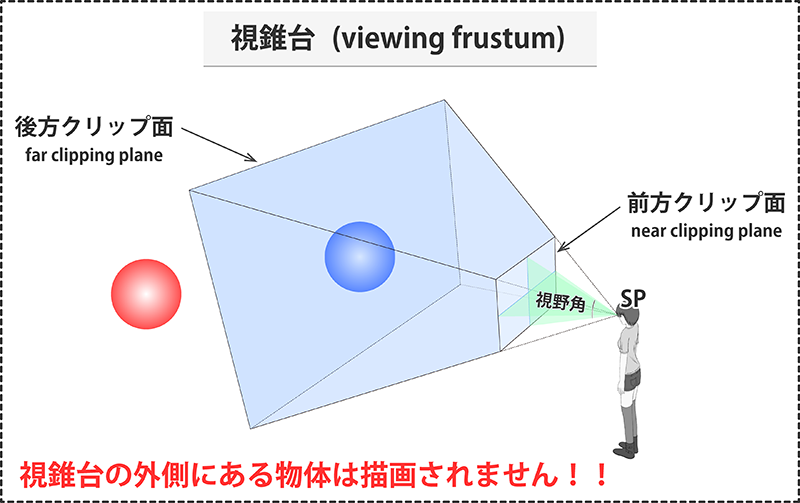
透視図法では画角(=視野角)を視覚的に表現するために視円錐を用いますが、3DCGでは左図に示すような角ばった視野が使われることがあります。 この形は四角錐(ピラミッド型)の先端を切り取ったものに相当し四角錐台と呼ばれますが、円錐に対して視円錐という言葉があるように、錐台型の視野は視錐台(しすいだい)といいます。
視円錐との大きな違いとして、前後のクリップ面があります。視円錐は円錐の内側であれば先端から無限の彼方まで視野内に入りますが、3DCGにおけるカメラは視錐台の内側しか見えません。 つまり前方クリップ面より手前と後方クリップ面より奥にあるオブジェクトは描画対象にならないのです。左図においては、視錐台の内側にある青いオブジェクトは描画されますが、外側にある赤いオブジェクトはたとえ視野角内に入っていたとしても描画されません。
このような視野が採用されている理由は、処理負荷の軽減にあります。 多くの3DCGアプリケーションは膨大なオブジェクトを扱う傾向にあり、特にゲームのようなリアルタイム性が要求される用途では、描画の負荷が問題になります。 視野を視錐台の内側に限定することで、描画対象オブジェクトを減らし、またZバッファ上でのZ値の精度を向上させることができます。(詳細は後述します)
視錐台はZバッファ法と併用して使われることが多いです。 Zバッファ法とは重なり合う物体のどちらがより手前にあるかを判定するためのアルゴリズムであり、画面上の画素に物体を描き込む際に、その物体の奥行をZバッファと呼ばれる記憶領域に格納しておき、同じ画素に別の物体が描かれようとした際には、その物体の奥行とZバッファ上の奥行を比較して、より手前であれば描画するという選択を行うものです。
比較的高速に行えることからゲームなどのリアルタイム用途に利用されています。 しかしZバッファ法を使わないのであれば、後述する射影変換は必須要素ではなくなるため、視野形状も錐台に拘る必要はなくなります。 視野形状はレンダラーの実装次第であり、視錐台はあくまでもその一形態となります。
透視投影の3次元射影変換
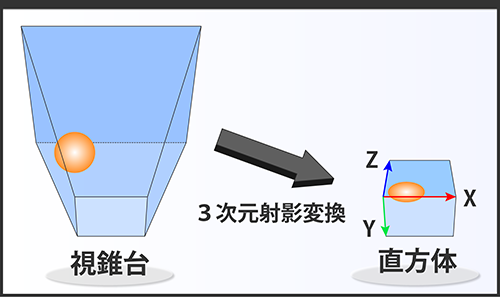
3DCGで透視投影を実現する際によく用いられる方法として、視錐台の変形があります。 この処理を3次元射影変換といい、視錐台は直方体に変換されます。 このとき、視錐台の内外にある物体も同じ法則で変換がかかります。
厳密には、この変換自体が透視投影を行っているわけではないのですが、変換後のオブジェクトはXY平面に平行投影するだけで、透視投影としての像を得ることができます。 またZ座標にも重要な役割があり、複数ある物体のどちらがより手前にあるかを判定するために使われます。画面には最も手前にある物体のみが描画されます。(Zバッファ法と呼ばれます)
この変換に関連して、視錐台のクリップ面の位置が重要になります。前方クリップ面をより手前に出したり、後方クリップ面をより奥に下げると、視錐台の体積は増えることになりますが、 変換後の直方体の体積は一定であるため、元の視錐台の体積が大きければ大きいほど、視錐台内部に強い圧縮が掛かります。
もちろん物理的な力が加わるわけではないため、内部の物体が破損するわけではないですが、データの上で奥行を表すZ値の精度が危ぶまれます。 仮にこの値を16ビットで表すとすれば65536通りの奥行しか表現できません。 変換前の視錐台の奥行が広ければ広いほど、実際には異なる奥行を同じ奥行と誤判定してしまう可能性があります。 結果として表示が乱れます。(この問題はZファイティングと呼ばれます)
基本的対策としては、むやみに大きい視錐台を作らないようにします。特に前方クリップ面をカメラに近づけすぎると、Z値の精度が著しく低下するため、前方クリップ面の位置は可能な限り下げてください。
参考ページ
数学 - 射影幾何学2 (背景変換と射影変換)
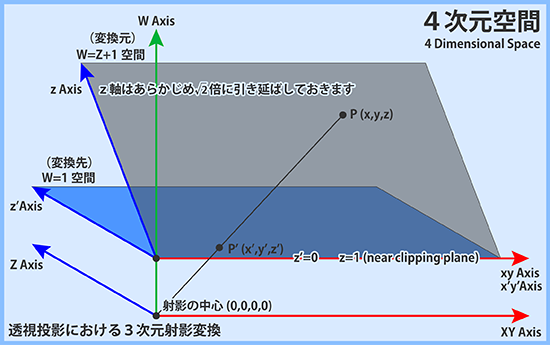
3次元の射影変換を行うには、3次元空間全体を4次元空間に配置する必要があります。 下図はその概念図となりますが、通常の手段では4次元空間を描くことができませんので、X軸とY軸を束ねてXY軸と表現しています。 下図において平面として描かれているものが、3次元空間を表しています。
ここで透視投影に相当する視錐台の変形(視錐台→直方体)を行うために次の空間モデルを考えます。 W=Z+1空間に変換元の3次元空間を置き、変換先の3次元空間をW=1空間とします。 視錐台の前方クリップ面はz=1とし、後方クリップ面は無限の彼方、すなわちz=∞にあるものとします。 変換後の両者はz'=0およびz'=1に正規化されることを目指します。
ここで変則的な座標軸の取り方をします。W=Z+1空間におけるz=1を図に示す赤い軸の上に置き、同じ位置にW=1空間におけるz'=0を置くものとします。 さらにW=Z+1空間のz軸はルート2倍しておきます。要するにWが1増えるたびに、zも1増えるような座標軸の取り方をします。(そのような射影変換が事前にかかっていると考えてください)
この状態で射影の中心を原点に置き、変換元の任意の点P(x,y,z)が、点P'(x',y',z')に変換されるとき、両者の関係式は次にようになります。
y'=y/z
z'=1-1/z
よってx'とy'に関しては、透視投影が掛かっていることが確認できます。 また、z'は前方クリップ面において0、後方クリップ面において1となり、正規化されていることが分かります。