1.ユークリッド幾何学
ユークリッド平面(Euclidean plane)
平たく言えば座標を2つの実数(X,Y)で表現できる普通の平面のことです。 中学校や高校で習う平面は、基本的にユークリッド平面です。
ユークリッド空間(Euclidean space)
座標を3つの実数(X,Y,Z)で表現できる普通の空間のことです。 空間は必ずしも3次元とは限りませんが、多くの場合3次元を指します。
2.射影幾何学
射影平面(projective plane)
ユークリッド平面に対して、無限遠点(その集合である無限遠直線を含みます)という概念を追加した平面です。
射影平面上では任意の2直線がただ1つの交点を持ちます。
ユークリッド平面では平行な2直線が交点を持たないという例外がありましたが、射影平面にはそのような例外がありません。なぜなら平行な2直線は無限遠点という交点を持つからです。
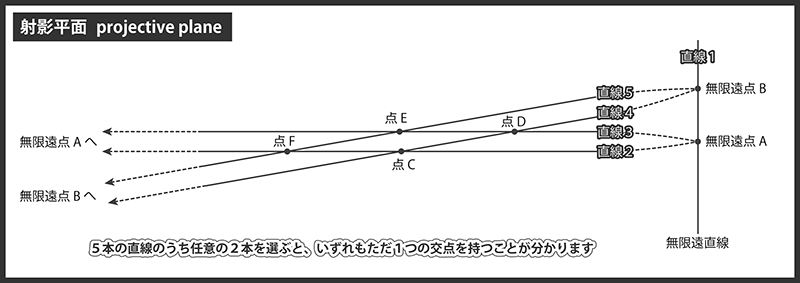
射影平面上の任意の直線は、その向きに応じた無限遠点をただ1つ持ちます。この無限遠点はある直線の左右両側に1つずつあると考えるのではなく、左右の無限遠はつながっており、同一の点に到達すると考えるのがポイントです。
射影空間(projective space)
ユークリッド空間に対して、無限遠点(その集合である無限遠直線や無限遠平面を含みます)という概念を追加した空間です。 透視図法は、射影空間上の任意の点と視点(SP)を直線で結び、その延長線上にある射影平面(PP)上の点に投影する作図法であると言えます。
無限遠点(point at infinity)
空間上において、無限の彼方を表す点のことです。無限遠点を導入した空間のことを射影空間といいます。 平行な2本の直線は同じ無限遠点を持ちますが、向きの異なる2本の直線は異なる無限遠点を持ちます。 要するに無限遠点は1つの向きに対して、1点存在します。
透視図法では、無限遠点は消失点として投影されます。 すなわち投影対象の空間を射影空間と考えると、この射影空間上の無限遠点はPP上では消失点と呼ばれる(無限遠点でない)通常の点になります。
無限遠直線(straight line at infinity)
ある射影平面において、すべての無限遠点をつなぎ合わせたものを無限遠直線といいます。
無限遠直線は無限遠点の集合であり、平面上の無限遠点を漏れなく含んでいます。
ある平面における無限遠点の集合を、半径が無限大の円と考えるのではなく、直線と考えるのが重要ポイントです。
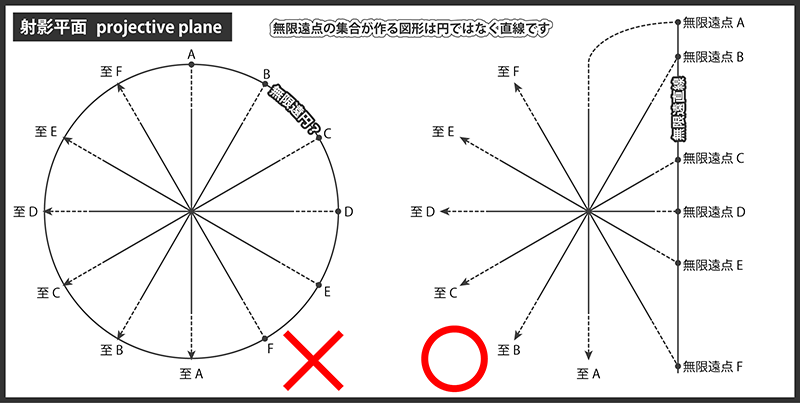
1つの射影平面に対して無限遠直線は1本しかありませんが、射影空間上においては無数に存在します。
概念は点のときと同様で、平行な2つの平面は同一の無限遠直線を持ちますが、向きの異なる2つの平面は異なる無限遠直線を持ちます。
透視図法では、無限遠直線は消失線として投影されます。 すなわち投影対象の空間を射影空間と考えると、この射影空間上の無限遠直線はPP上では消失線と呼ばれる(無限遠直線でない)通常の直線になります。
無限遠平面(plane at infinity)
ある射影空間において、すべての無限遠直線をつなぎ合わせたものを無限遠平面といいます。 無限遠平面は無限遠直線の集合であり、無限遠点の集合でもあります。1つの射影空間に対して無限遠平面はただ1つしかありません。


