円の描き方
円の透視投影である楕円、放物線、双曲線、直線の作図法を以下にまとめます。 これらの作図法を駆使すれば、考え得るあらゆるパターンのパース円を描くことができます。
| 作図法 | 座標系 | 図形種別 | 要点と特徴 |
|---|---|---|---|
| 直接法 | 1点透視 2点透視 | 楕円 放物線 双曲線 | 透視図上での楕円の中心や長短軸の向きを求めて、直接的に楕円を描く作図法です。直で楕円を描くため、素早く描けるのが最大のメリットです。欠点として精度が不完全であることが挙げられますが、足線法やシアーを併用すれば、厳密な精度を確保することができます。放物線や双曲線の描き方も確立できたので、以下で説明します。 (直接法という名称は本サイトが勝手に付けました) |
| 足線法 | 1点透視 2点透視 | 楕円 放物線 双曲線 直線 | 平面図を元に透視図上での投影点を求め、それらを結んで楕円等を完成させます。放物線や双曲線も描ける万能な方法です。本サイトでは透視図を元に平面図を起こす方法も示します。 |
| 正多角形近似 | 1点透視 2点透視 | 楕円 | 正多角形の頂点を求め、それらを結ぶことで楕円を描く方法です。正八角形であれば比較的簡単に描けます。作図に際して、外接正方形が必要となります。放物線や双曲線パターンは外接正方形を描くことができない(※1)ため、基本的に本作図法は使えませんが、正方形の奥半分を描く等で対応できる場合があります。 |
※正円になるパターンは、パースの技術抜きで普通に描けるため、ここでは扱っていません。
※1:観測者の後ろに回り込むため、透視図上では無限大の大きさになり、なおかつ全体が入りません。
円の描き方(直接法・楕円)
スライドP19は傾斜面上の楕円を示しますが、それ以前のページの楕円とまったく同じ形状をしています。
奇妙な現象に思えるかもしれませんが、同じ被写体に対して、カメラを水平に向けた場合Aと、傾けた場合Bで、まったく同じ見た目になることがあるのです。
(ただしAとBは異なる視点です。また被写体は平面に限ります)。
ここでカメラを傾けることは世界が傾くことと同義であると考えてください。
つまり透視図法では、傾斜があってもなくても(被写体が平面である限りは)本質的に見え方は変わらないということです。
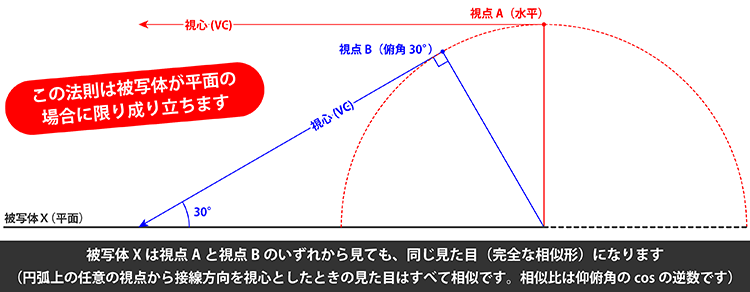
詳細は応用の章で解説していますが、透視図法における平面は正対面を除けば、消失線が視心を通るか通らないかの2種類しかありません。 また2種の平面間で図形が相似となるため、上のスライドで示す1つの作図法だけで、あらゆる平面上の円を作図できます。
手順が多少複雑化しても良いのであれば、円の性質2で紹介した方法が使えます。
円の描き方(直接法・放物線&双曲線)
円の描き方(足線法)
ここで示す手順は、概要の章で紹介した透視図の定義による作図と完全に同じものです。 3枚の図(透視図と平面図と側面図)を重ねて描いているので、直感的に分かりにくいかもしれませんが、やっていることは同じです。 混合図の節で説明した通り、図を重ね合わせるのは作図線の数を減らすためですので、分かり難ければ3枚の図を別々に描いて練習してみてください。
なお名称を足線法とすることには悩みましたが、透視図の定義通りに視線を引いて作図する方法は、視線と足線がほぼ同じ意味を持つ補助線であることから、広義の足線法と解釈して問題ないと判断して、そう命名しました。 公に通用するかは別問題ですので、その点は注意してください。
スライドの後半で傾斜面への作図法が傾斜していない場合と同一であることを示していますが、1つ注意すべきことがあります。それは傾斜面に作図する場合は平面図形しか描けないという点です。90°視円錐を使う本来の作図法であれば、例えば立方体や円柱などの高さのある物体を描くことが可能ですが、傾斜消失点を中心とする円を使って作図する場合は、正方形や円などの高さのない図形しか描けません。もちろん、その図形は消失線と対応する傾斜面に含まれることが絶対条件です。
円の描き方(正多角形近似)
ある平面上における円の性質を考えます。円は平面内でどのような角度の回転を掛けても、形状に変化が生じません。 すなわち消失線が視心を通る平面上においては、1点透視図の円と2点透視図の円は、同一形状であることを意味します。 円に外接する正方形は1種類ではなく、様々な角度で描画することができます。つまり2点透視図の正方形に内接する円を描きたい場合、一旦正方形を1点透視図になる向きまで回転させたあと、そこに内接する円を描けば良いことになります。 (難度は上がりますが、回転を掛けずに直接描くこともできます)
また消失線が視心を通らない面(2点透視図の側面や3点透視図)にある円の場合も、測点法や介線法、対角消失点法を駆使すれば、正多角形を描くことができますので、本質的には1点透視図のときと同じ作図法が通用すると言えます。


