円錐曲線と離心率
楕円、放物線、双曲線は円錐を切断したときに現れる図形であることから円錐曲線と呼ばれますが、 同一の立体から発生する曲線なだけはあり、その図形的性質には大きな類似性が見受けられます。
ここで離心率というものを紹介します。
これは３種の円錐曲線を同一図形として扱ったときのパラメータのようなものです。
円錐曲線は、焦点、準線、離心率の３要素を与えることで作図することができます。
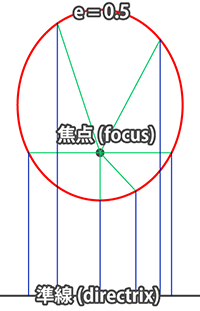
簡単に言うと、曲線上の点は、どこを取っても準線までの距離と焦点までの距離が同じ比率eになります。
例えば離心率e=0.5の場合、準線までの距離（青い線）を1とすると、焦点までの距離（緑の線）はその半分の0.5になります。
ここで焦点と準線はどのような取り方をしても、図形の形状に影響を与えないことに注意したいところです。 なぜなら左図の状態を標準形と呼ぶことにすると、他のどのような配置に対しても、拡大縮小、平行移動、回転を行うことで標準形に変換できるからです。 結局のところ、円錐曲線の形を決めているのは離心率だけであり、離心率の同じ２つの円錐曲線は相似であるという重要な性質が導出できます。
離心率は１未満のときが楕円、１が放物線、１を超えると双曲線になります。 離心率が０のときは図形を描くことができませんが、 離心率が非常に小さいとき(0.0001等）は焦点を中心とする（ほぼ正円な）楕円になることから、円として扱います。
円錐曲線を描く際には、表面的な図形種別よりも、むしろ離心率に注意を払うべきと言えます。
なぜなら同じ楕円という分類でも、離心率０付近（ほぼ正円）と１付近（ほぼ放物線）では形状が大幅に異なるからです。
また離心率0.99の楕円と1の放物線と1.01の双曲線は、焦点の付近だけを取り出せば、並べて見ても見分けがつかないほど同じ形をしています。
| 図形 | 離心率e | 特徴 | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 円 | e=0 | 円は楕円の特殊な形であり、その扁平率が０のものを指します。 | |||||||||||||||||||||||||||
| 楕円 | 0<e<1 | 離心率は楕円の扁平率（潰れ方）と１対１に対応します。つまり同じ扁平率を持つ楕円は、同じ離心率であり、逆も成り立ちます。離心率が０に近いほど正円に近く、１に近いほど潰れた楕円になります。 | |||||||||||||||||||||||||||
| 放物線 | e=1 | 放物線は離心率の隣合う２つの図形（楕円、双曲線）の性質を併せ持っています。つまり限りなく潰れた楕円や角の鋭い双曲線と同じような形状をしています。 | |||||||||||||||||||||||||||
| 双曲線 | 1<e | 離心率は漸近線のなす角（双曲線のある側の角度とします）と１対１に対応します。つまり２つの漸近線のなす角が同一の双曲線は、同じ離心率であり、逆も成り立ちます。離心率が１に近いほど頂点の鋭い曲線になり、値が大きいほど緩やかな曲線になります。無限大付近ではほぼ準線と一致する直線状になります。
|
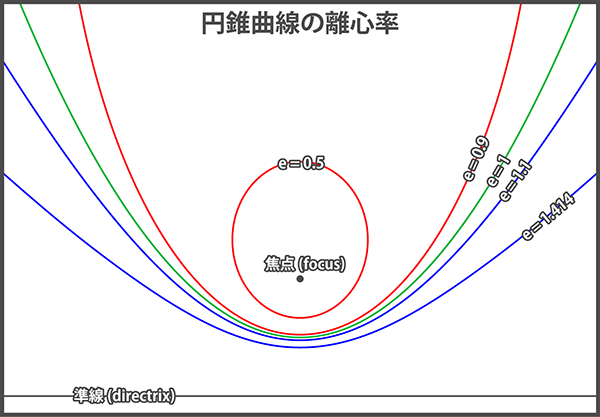
離心率は円錐曲線の形状を決める唯一のパラメータです。
よって離心率が同じであれば、必ず同じ形状（相似）になります。
逆に離心率の異なる２つの円錐曲線が相似になることはありません。
円については、すべての円が相似であることは形状的に明らかですが、放物線に関しても離心率が１に固定されていることから、あらゆる放物線は相似であるという結論になります。 次に楕円ですが、楕円の離心率は扁平率（へんぺいりつ、楕円の潰れ方を表す値）と対応しているため、扁平率が同じ楕円は相似となります。これも直観的にわかる事実だと思います。
問題は双曲線です。双曲線の相似性はすぐには見抜けないと思いますが、こちらも離心率による判断ができます。
双曲線の離心率は２本の漸近線のなす角と対応します。角の大きさで双曲線のとがり具合が決まり、
角度さえ同じであれば、完全に同じ形状（相似）になります。
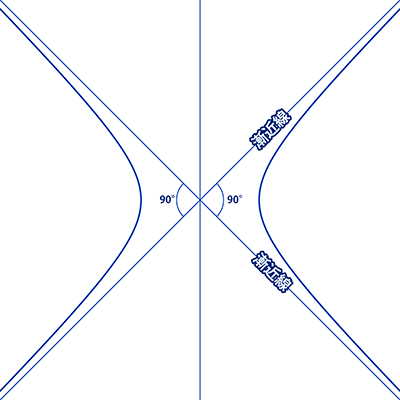
例えば、すべての直角双曲線(*)は離心率がルート２ですので、互いに相似形であると言えます。
* 漸近線のなす角が90°の双曲線（左図参照）
離心率が近い楕円、放物線、双曲線は、互いの図形を近似として扱うことができます。 たとえば、楕円ツールで細長い楕円を描き、とがっている側の先端を切り取れば、近似的な放物線とみなすことができます。 また難易度の高そうな放物線と双曲線も、ひな形さえ用意できれば、それを変形することで、あらゆる放物線や双曲線を作り出せます。以下で詳しく説明します。
放物線の性質と描き方
上記手順では、コピー元となる正確な放物線があることを前提としています。 ベジェ曲線を使えば簡単に作図できますが、対応するソフトがない場合は、どこかから拾ってくる手もあります。 入手した図形が正確な放物線であるかどうかは、5ページ目に示す拡大を行うことで確認できます。 拡大後にO～A間の曲線の形状が変化した場合は、正しい放物線ではありません。 ３次ベジェ曲線で描かれた正確な放物線はツールの章に置いてあります。ダウンロードしてご自由にお使いください。
説明の流れから混乱を招く恐れがあるので、補足しておきます。 縦横比の異なる拡大縮小は相似の操作として認められていませんが、現実の作図では相似の証明をするわけではないので、比率の異なる拡大縮小をしても問題ありません。 縦横比を変更しても、放物線は放物線であり続けます。 むしろ縦横比は変更しなければならないケースの方が多いです。5ページ目に示すように２点O,Aを通る放物線を拡大する際は、横と縦の倍率が２乗の関係になるよう拡大する必要があります。 これを同じ比率で拡大してしまうと、y=ax^2のaの値が変化してしまうため、点Aを通らなくなってしまいます。
多くのベクターグラフィックスソフトはベジェ曲線と呼ばれるＮ個の制御点を使用した曲線の描画方法を採用しています。
３次ベジェ曲線の場合、制御点は４個必要であり、高々３次までの曲線を引くことができます。
厳密な精度を持つ円錐曲線を描こうとした場合、通常のベジェ曲線で正確に表現可能なものは放物線に限られ、円、楕円、双曲線は近似的な表現しかできません。
（有理ベジェ曲線やNURBS曲線であれば、正確に表現できます）
双曲線の描き方
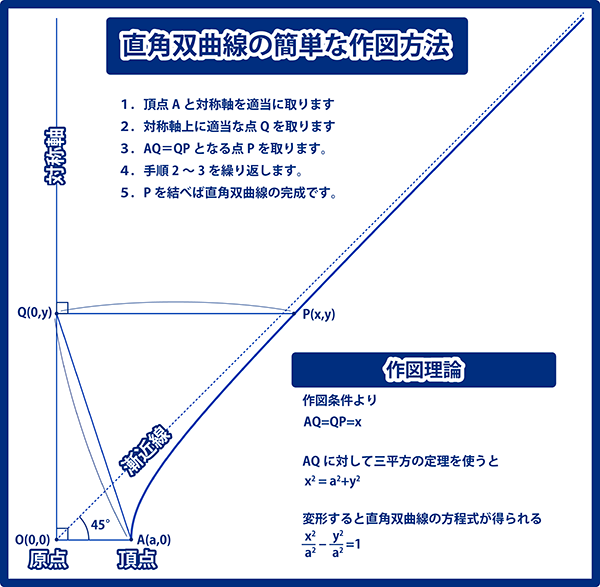
直角双曲線の作図方法を以下に示します。すべての直角双曲線は相似ですので、これ以外の形をした直角双曲線は存在しません。 またこの双曲線をＸ軸（またはＹ軸）方向に対してのみ拡大縮小すれば、直角以外のあらゆる角度の双曲線を作ることができます。
この作図法のメリットとして、漸近線もセットで作図できることが挙げられます。漸近線は原点から45°方向に引けばよいです。原点は頂点から対称軸に対して垂線を下した位置にあります。
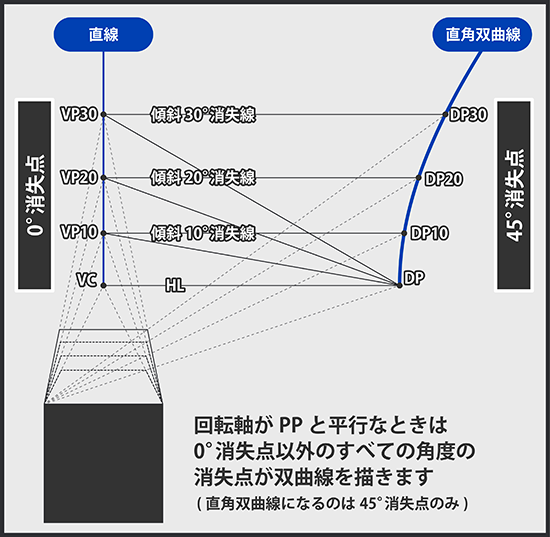
ある平面に対して対角(45°方向)消失点を考えます。この平面を傾斜させていくと対角消失点も移動しますが、その軌跡は（回転軸がPPと平行であれば）直角双曲線を描きます。 これが上図の作図方法を思いついたきっかけです。
ちなみに軌跡が描く図形は回転軸の方向によって変わり、対角消失点について言えば、PPに対して斜め45°のときは放物線、それ以上の角度がつくと楕円になります。(0°<θ<45°は直角以外の双曲線）。
軌跡が円錐曲線となるのは、SPから見て各消失点を指すベクトルの先端が回転によって円を描くためです。（結局、円の透視投影と同じなわけです）
参考文献：パース２！マンガでわかるもっとディープな遠近法 P17
双曲線も放物線同様、ひな形を拡大縮小、平行移動、回転させることで、あらゆる双曲線と重ね合わせることができます。
ただし放物線とは異なり、すべての双曲線は相似ではなく、漸近線のなす角が同じ双曲線が相似であるというだけなので、その点に注意を払う必要があります。
漸近線のなす角を変えるには、縦横比を変えて拡大縮小すれば良いです。 必ず標準形に対して、座標軸に沿った向きに拡大縮小させてください。
漸近線の角度を狙った値にしたい場合は、タンジェントの値で拡大縮小します。元が直角双曲線(90°)である場合に120°に変換する場合は、拡大率をtan(30°)≒0.577にします。θに変換する場合の拡大率はtan((180°-θ)/2)です。
ひな形を拡大縮小、平行移動、回転させて、指定した点を通る双曲線を作るのは意外と難しいです。 なぜなら双曲線は放物線と異なり、対称軸を固定した上で１点を指定しても、（漸近線の角度が未定であれば）曲線の形が一意に決まらないからです。 コツとしては漸近線も含めた図形として考えることです。双曲線は漸近線と頂点さえ一致すれば、曲線自体も完全に一致します。
もう１つの注意点はひな形の長さです。放物線の場合は、拡大縮小を繰り返すことで好きなだけ曲線を延長することができますが、双曲線はひな形が持つ長さ以上の長さを作ることができません。 よって、長さが足りない場合はひな形を改造する必要があります。
概ね正確な双曲線はツールの章に置いてありますので、ご自由にお使いください。
