１．円錐曲線
円錐(cone)
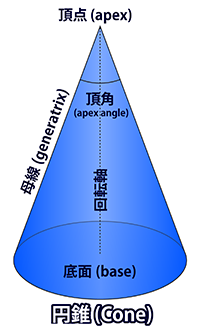円錐は回転軸と平行でない直線を回転させたときにできる３次元図形です。
回転対象の直線を母線と呼び、母線と回転軸の交点を頂点と呼びます。
また母線の頂点側でない端点を回転させたことによってできる円を底面と呼び、母線そのものの回転で作られる面を側面と呼びます。
頂点と円周上の任意の点を結んでできる直線もまた母線と呼ばれます。 円錐を回転軸を通る平面で切断したときにできる二等辺三角形の頂角を、この円錐の頂角と呼びます。 頂角は任意の２本の母線のなす角のうち最大となる角度であり、母線と回転軸のなす角の２倍でもあります。 透視図法で「90°視円錐」と言った場合、この90°は頂角を指します。
※頂角は「側面の展開図（扇型）の中心角」という定義も存在するようです。専門書での記述を確認をし、後日反映させます。(2015/03/30)
円錐曲線(conic section)
円錐の側面を任意の平面で切断したときにできる曲線を円錐曲線と言います。 具体的には、円、楕円、放物線、双曲線のいずれかです。 ただし頂点を含む平面で切断した場合は、点、直線、２直線のいずれかになります。
底面と切断面のなす角をθとし、底面と母線のなす角をαとすると、下表の通りとなります。図形1は頂点を含まない平面で切断した場合、図形2は頂点を含む平面で切断した場合を指します。 円錐は直円錐であるとします。
| 平面の向きθ | 図形1 | 図形2 |
|---|---|---|
| θ=0° | 円 | 点 |
| 0°<θ<α | 楕円 | 点 |
| θ=α | 放物線 | 直線 |
| α<θ≦90° | 双曲線 | ２直線 |
円錐曲線の離心率はθと１対１の関係があります。 つまり平行な２つの切断面によって作られる２つの円錐曲線は同じ離心率を持ちます。 よって、その２つの円錐曲線は相似です。 これは透視図法的に考えても明らかです。 PPはどの奥行に置いても投影形状に影響を与えないことから、円錐をある平面で切断したときと、その平面と平行な平面で切断したときの断面の形状が一致しなければならないことになります。
またθに対して、離心率は単調増加します。つまりθ=0°のとき離心率０、θ＝αで離心率１、θ=90°で最大値を取ります。 ある円錐に対する離心率の最大値は無限大ではなく、漸近線のなす角が頂角と一致する双曲線の離心率が最大です。 頂角を180°に限りなく近づけると、離心率の最大値は無限大になります。
楕円(ellipse)
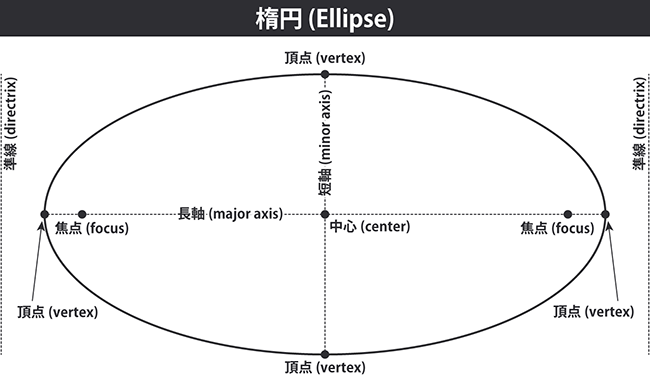
２つの焦点からの距離の和が一定である点の集合が楕円です。 円錐曲線の定義「準線からの距離と焦点からの距離が一定比率である点の集合」も満たしており、 楕円の場合は準線からの距離よりも焦点からの距離の方が短くなります。
楕円上の２点を両端とする線分のうち、最も長いものを長軸、短いものを短軸と呼びます。 長軸と短軸は中心を通り、中心で直交します。また長軸は準線と垂直であり、短軸は準線と平行です。 ２つの焦点は長軸上に乗ります。長軸や短軸と楕円との交点を頂点と言います。 短軸上の頂点から焦点までの距離は、長軸上の頂点から中心までの距離と一致します。
長軸と短軸の長さを一致させると円になるため、円は楕円の特殊型であると言えます。
このとき２つの焦点は円の中心と一致し、準線は無限遠直線となります。
カメラ前方に収まる円を透視図法で描くと楕円になります。
放物線(parabola)
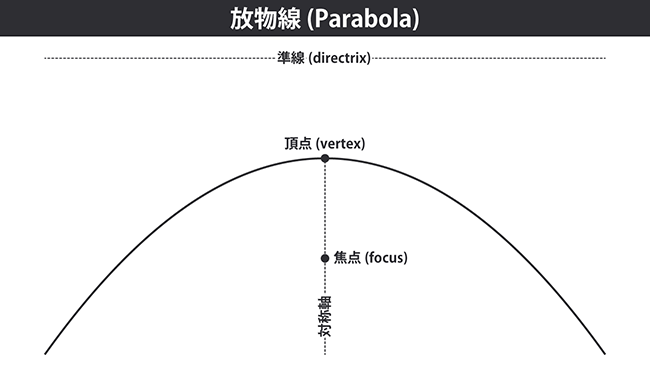
重力下で物を放り投げたときに描く軌跡が放物線です。 数学的定義は「準線からの距離と焦点からの距離が等しい点の集合」となります。 放物線はある直線を境に折り返すと重なる図形です。この直線を対称軸といいます。 対称軸と放物線の交点を頂点と呼びます。 射影平面上では、対称軸と放物線は無限遠点でも交わります。
カメラからゼロ距離の平面（SPを通りPPと平行な平面）に接する円を透視図法で描くと放物線になります。
双曲線(hyperbola)
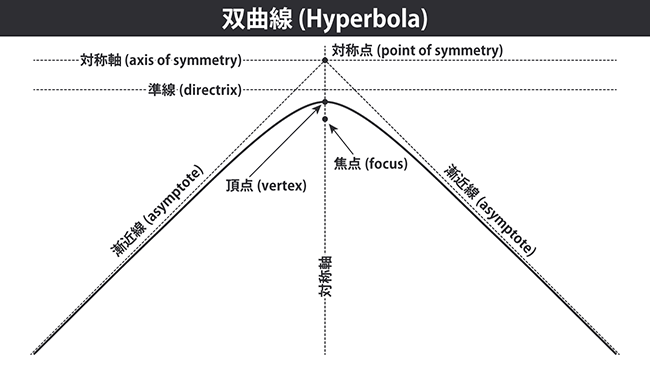
２つの焦点からの距離の差が一定である点の集合が双曲線です。 （２つ目の焦点は図示していませんが、対称点を中心とした反対側にあります）。 円錐曲線の定義である「準線からの距離と焦点からの距離が一定比率である点の集合」も満たしており、 双曲線の場合は準線からの距離に対して焦点からの距離の方が長くなります。
双曲線は２本の曲線が組になっており、下図はそのうちの１本のみを描いています。 この２本の曲線は対称点を中心として180°回転させたときに重なる点対称です。 また２つの対称軸を境に折り返したときも重なるため、線対称でもあります。 対称軸と双曲線の交点を頂点と呼びます。 また２つの焦点は対称軸上にあります。 双曲線を無限の彼方まで伸ばすと、ある直線に限りなく近づきます。この直線を漸近線と呼びます。 双曲線と漸近線は通常の平面では接点を持ちませんが、射影平面上では無限遠点で接点を持ちます。
下図は漸近線のなす角が90°の双曲線であり、これを直角双曲線と呼びます。直角双曲線においては、準線が焦点と対称点から等距離になります。
カメラの後方にまで広がる巨大な円を透視図法で描くと双曲線になります。
２．角度
余角(complementary angle)
足して90度になる2つの角があるとき、一方の角はもう一方の角の余角といいます。 例えば、20度の余角は70度です。
補角(supplementary angle)
足して180度になる2つの角があるとき、一方の角はもう一方の角の補角といいます。 例えば、50度の補角は130度です。
鋭角(acute angle)
90°よりも小さい角度を、鋭角といいます。
鈍角(obtuse angle)
90°よりも大きく180°未満の角度を、鈍角といいます。
直角(right angle)
90°である角度を、直角といいます。
３．三角形
鋭角三角形(acute triangle)
３つの角すべてが鋭角である三角形です。
鈍角三角形(obtuse triangle)
１つの角が鈍角である三角形です。残り２つの角は鋭角になります。
直角三角形(right triangle)
１つの角が直角である三角形です。残り２つの角は鋭角になります。
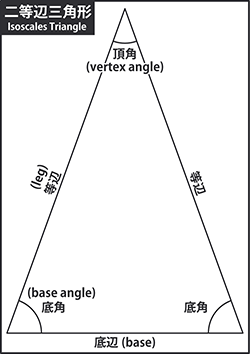
二等辺三角形(isoscales triangle)
２辺の長さが等しい三角形です。この２辺によって挟まれない２つの角は同じ角度になります。
長さの等しい２辺を等辺、残る１つの辺を底辺、角度の等しい２つの内角を底角、残る１つの角を頂角と呼びます。
直角二等辺三角形(isoscales right triangle)
直角三角形と二等辺三角形の両方の性質を併せ持つ三角形であり、２つの底角は共に45°です。
正三角形(equilateral triangle)
３辺の長さが等しい三角形です。３つの角も等しくなり、すべて60°となります。
