二等辺三角形
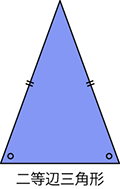
二等辺三角形はみなさんご存じだと思いますが、その名が示す通り2つの辺の長さが等しい三角形です。
図に示す通り、2つの角度も等しくなる性質があります。裏を返せば、2つの角度が等しい三角形は、
2辺の長さが等しくなることを意味します。
二点透視図では、二等辺三角形のこの性質を用いて作図を行います。
透視図における二等辺三角形
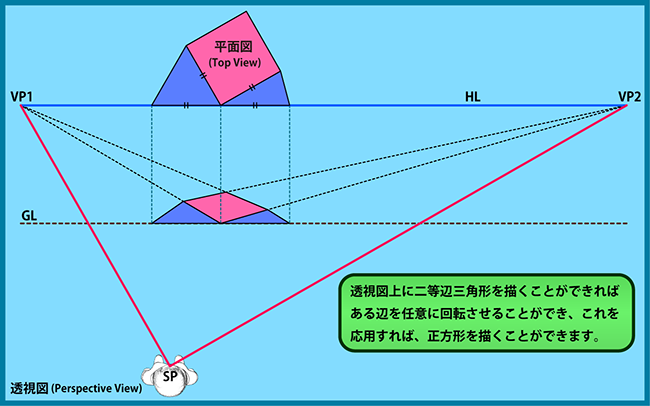
対角消失点を使えば、正確な正方形を描くことができますが、思い通りの寸法で描画することができないという問題点がありました。
しかし、二等辺三角形を作図に応用すれば、この問題が解決します。
測点
PAGE 1/x
測点法による正方形の描き方および辺の回転
[Click] 1点透視図における測点は?
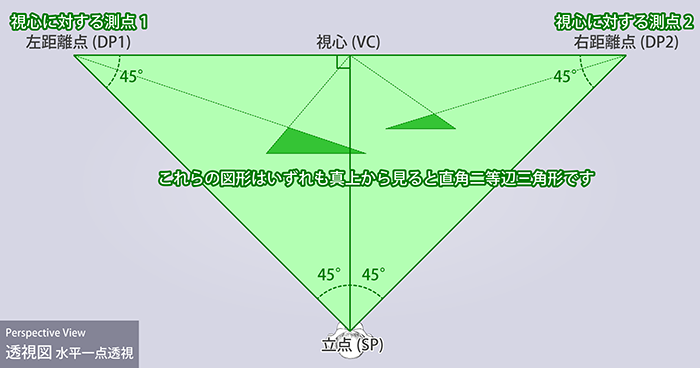
1点透視図では測点という話題が出てきませんでしたが、1点透視図には測点は無いのでしょうか? 1点透視図における消失点は視心に限られますので、視心に対する測点を考えてみましょう。 2点透視図と同じ作図ルールで測点を求めると、距離点が測点と一致することが分かります。 よって、1点透視図における測点は距離点であると言えます。
視心と距離点を使って作図された三角形はただの二等辺三角形ではなく、直角二等辺三角形になります。
[Click] 1つの消失点に対して測点は2つ存在するのでは?
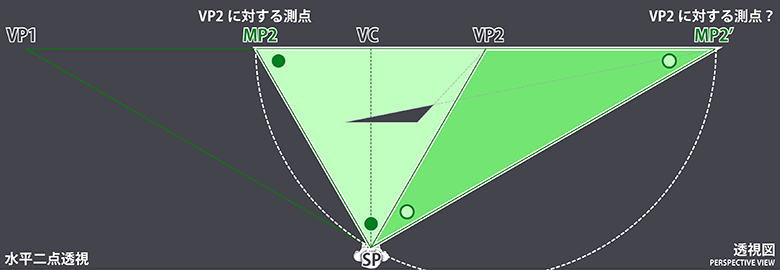
2点透視図における測点の作図ルールは、基本となる消失点を中心としSPを通る円を描いたあと、水平線との交点を求めるというものでした。
ここで円と水平線の交点は2点存在しますが、そのうちの一方、すなわち視心を跨ぐ側の交点を測点と呼んでいます。
ところが逆方向にも交点はあり、そちらの消失点を使っても二等辺三角形を作図できそうです。
しかし視心を跨がない側の消失点は画面から遠い位置にあり、作図上不便であるため、一般的には測点として利用されることはありません。


スポンサーリンク
amazon co.jp アソシエイト
