3つ目の消失点の取り方
消失点の発生位置(立体図)
3個目の消失点の取りうる範囲
3点透視における3個目の消失点は、どこに配置しても良いという性質のものではありません。 2点透視での視心の位置は2つの消失点の間にできるという法則がありました。 そして3点透視の視心および3点目の消失点は、2点透視での視心と同じ垂直線上に発生します。 したがって、下図のようにVP1とVP2が配置されている場合、 VP1より左側およびVP2より右側にVP3が来ることは絶対にありません。 さらにVP1とVP2を直径とする円の内側に来ることもありません。 なぜなら、VP3はSPより外側にしか発生しないからです。 以上を踏まえると、VP3の取り得る範囲は、青で塗り潰された領域内のみであることが分かります。 (図は途中で途切れていますが、青い領域は無限に上方向および下方向に伸びています)
なお、この領域内にVP3を取った場合、3つの消失点を結んでできる三角形は必ず鋭角三角形になります。 領域の外にVP3を取ることはできませんが、仮に領域の境界部にVP3を取れば直角三角形になり。 領域外に取れば鈍角三角形になります。 つまり消失点を結んでできる三角形が直角三角形や鈍角三角形になった場合は、 三点透視の消失点としてはありえない組み合わせであるということになります。
ありえない組み合わせで作図するとどうなるか
消失点同士を結んでできる図形が、直角三角形または鈍角三角形になることはありえないということが分かりましたが、 仮にその事実を知らず、直角三角形や鈍角三角形の消失点を取ってしまった場合、作図にどのような支障をきたすのでしょうか?
結論を言うと、そのような消失点を使って直方体を描こうとしても描けません。直角が出なくなります。
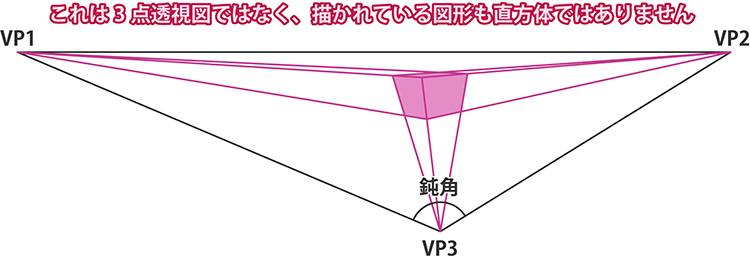
上図の図形は直方体ではなく、隣り合う辺が直交していない平行六面体です。 3つの消失点を結ぶ三角形が鈍角三角形となっていることから、3点透視図ではない「何か」になります。 換言すると「この3点を、互いに直交する3軸の消失点とみなす視点(SP)が存在しない」となります。 3点透視図でなければ何点透視図なのか、という疑問が湧き上がるかもしれませんが、何点透視でもありません。 ○点透視という分類は、空間を構成する3つの座標系が直交している場合に使う表現であり、 上図は直交座標系ではない座標軸の取り方をしているため、○点透視という分類自体が不可能と言えます。


