地面とは何か?
アイレベルは地面に付随する概念です。地面が定義できなければ、アイレベルもまた定義できません。 ここで1つの疑問が浮かび上がります。そもそも「地面」とは何を指すのでしょうか? 私たちは常に地面を見て生活しているわけではありません。 地下鉄のホームでは地面が見えませんし、遊泳中の宇宙飛行士には、周囲に地面が存在しないでしょう。 さて、地面とは何なのでしょうか?
実のところ平面であれば、どの面を地面と考えても構いません。 室内であれば床面を地面とするのが一般的ですが、天井を地面と置いても問題ありません。 普通は行いませんが部屋の側面を地面と置くことも可能と言えば可能です。 しかし、この場合側面の消失線が画面上では水平線ではなく垂直線となるため、 アイレベル上のすべての点は、地面の消失線上に現れるが正しい表現となります。 またアイレベルは地面に対して垂線を下して、その高さを定義することに注意してください。
少々特殊な例を出しましたが、一般的には重力と直交する平面を取るのが基本ですので、 本サイトでも特別な理由がない限りは、そのように考えるものとします。
地面のない場所では?
宇宙空間のような地面の存在しない場所ではアイレベルはどのように考えれば良いのでしょうか? アイレベルを扱う上での地面というのはあくまでも仮想の平面なので、描き手の都合の良い場所に平面を置き、 そこを地面として扱えば問題ありません。ただし、本当に星しか映らないような空間では、 仮想の地面をどこに置いたところで、アイレベルという概念の使いどころがありません。 地面から1mの高さと言ったところで、どこが1mなのか直感的に分からないからです。 これはビルの壁面を仮想地面とした場合も同じで、ビルの壁面から1mと言われても、ビルの近傍以外ではどこが1mなのか把握できないため、 そのように定義されたアイレベルに利用価値がありません。 アイレベルはあくまでも、パースを扱う上での便利な概念であるために導入されているにすぎないので、 地面を想定できない空間で無理にアイレベルという概念を持ち出す必要はありません。
視線の向きが地面と平行でない場合は?
しばしば問題になるのは、視線の向きが地面と平行でない場合のアイレベルの定義です。 そもそもアイレベルという用語自体の正確な定義があるかが定かではありませんが、 業界の慣習がどうあれ、本サイトでは常に次の定義を使います。
重力の働く惑星上に住む私たちは、鉛直線と平行または直交する人工の面を多数創り出しています。
したがって、鉛直線と直交する平面を地面とするのが最も理に適っています。
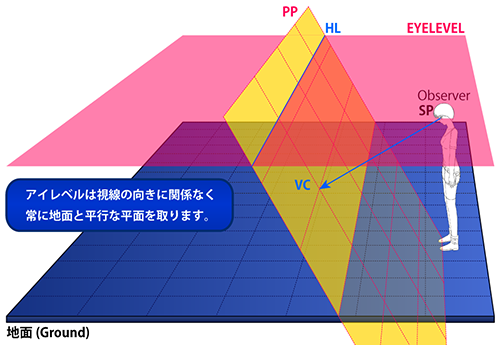
アイレベル=水平線か??
アイレベルと水平線は混同して扱われることが多々ありますが、両者は異なる概念です。 アイレベルは地面からのカメラの高さであり、水平線(HL)は地面の消失線です。透視図上では同じ位置に現れるため、 両者が同じものとして扱われることが多いですが、概念としては違うものであることに注意してください。
なぜアイレベルという概念を持ち出すのか
アイレベル上の点は同じライン上に集まりますので、作画の指針として大活躍します。 例えば、直立した同じ体格の人物を複数描く場合は、体の同じ部位が一直線上に並びます。 アイレベルが1mであれば腹部が、150cmであれば頭部が同じライン上に現れるでしょう。
しかし、アイレベル上にあるすべての点は、透視図上では水平線上に現れるという法則を聞くと、 なぜカメラの高さにそのような特殊な法則が成り立つのかを疑問に感じます。 実のところ、このような法則はアイレベルに限った話ではなく、SPを通るあらゆる平面に対して成り立つ概念です。 例えば、SPから10度上方向に向かう平面上にあるすべての点は、透視図上ではこの平面の消失線上に現れます。
しかしパースを扱ったほとんどの文献にはそのような説明は存在しないと思います。 なぜなら、そのような法則があると分かったところで、使い道があまりないからです。 唯一、地面から同じ高さにあるものが同じライン上に現れるという法則のみが役に立ちます。 なぜなら、私たちは地面から等距離にあるものは把握できるのに対し、SPから10度方向にあるものは把握できないからです。


