正方形を描く意義
パースで初めて何かを描こうとしたとき、最初に取り組むべき課題は正方形や立方体の作画です。 これらの図形は、あらゆるものを描く上での基礎となりますので、確実に押さえておかなければなりません。
下図は正方形を敷き詰めて空間を表現した例です。このように四角形を格子状に並べたものをグリッドと呼びます。
特に四角形が正方形の場合は正方形グリッドと呼ばれます。(以降は単にグリッドと呼びます)。
グリッドは空間表現の基本ツールですので、是非とも描き方をマスターしたいところです。
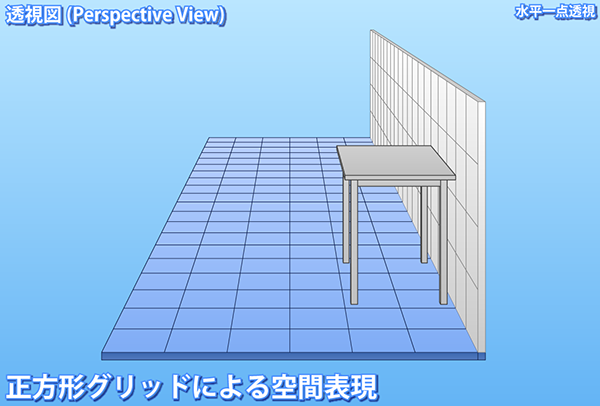
グリッドの何が便利かというと、マス目が物差しとして機能することです。上図の場合、正方形の一辺は25cmを想定しています。 グリッドのマスを目盛りとして使えば、図中に描かれた机の寸法は幅50cm×奥行75cm×高さ60cm程度であることが読み取れます。
本サイトでは、各○点透視の章で立方体(または正方形)の描き方という節を必ず設けています。
なぜ正方形や立方体をそこまで尊重しているかといえば、これらの図形が描けなければ、グリッドもまた描けないからです。
グリッドを作画するには、以下2つの基本技術を習得することが絶対条件となります。
- 正方形または立方体の作図
- 長方形の増殖および分割
1点透視図の性質
正方形の描き方を説明する前に、一点透視図の性質について簡単に説明しておきます。
1点透視図では奥行方向の辺はすべて視心に向かう性質があります。 この視心が1点透視図における唯一の消失点になるわけですが、奥行を決める際に使う距離点もまた消失点に違いありません。 なぜ1点透視図なのに、消失点が2個出てくるのかと思われるかもしれませんが、距離点はあくまでも作画補助用の消失点であり、正方形の対角線も補助線にすぎません。 絵の上に実際に現れる直線に限れば、その消失点は視心に限られます。
1点透視図では地面に置かれた正方形は(見かけ上)台形になる性質がありますが、この台形は適当に描いても正方形とみなせるのでしょうか? 答えはみなせます。どのような台形であっても、それが正方形となる視点(Station Point)が必ず存在します。よって、1点透視図で正確な正方形を描きたい場合、最初の1個に限れば見た目で判断して適当に描いても問題ありません。 もちろん2つ以上の正方形を描く場合は、対角線が同一の消失点(距離点)に収束するよう形を調整しなければなりません。
奥行方向の正方形の描き方
透視図法で難しいのは、奥行方向に向かうものを描画することです。 ここでは奥行方向の正方形の作画手順を説明します。


