通常、極は円の外側に取り、極から円に向かって接線を引いたときの接点同士を結ぶ直線を極線と呼びますが、概念を拡張すると、極を円の内側に取ることもできます。 このとき極線は円の外側に発生し、極線上の任意の点から円に向かって引いた接線に対して、その接点同士を結ぶ直線が極を通る、という性質を持ちます。

ここで下図を見ていただくと、極と極線の位置関係は見事に対になっていることが分かるかと思います。 すなわち、元々の極線の中点が極となり、元々の極を通る直線が極線となっています。 このときの極線の向きは、円の中心（または内部に取った極）と外側に取った極を結ぶ直線と直交します。


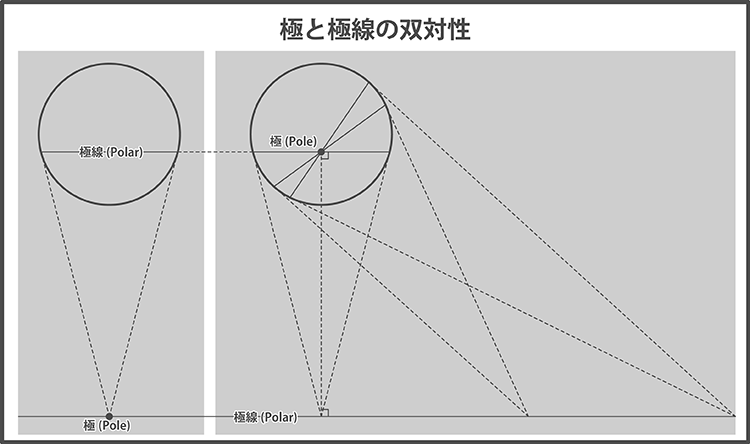
参考文献：射影幾何学入門 ―生物の形態と数学― (丹羽 敏雄著) P41～