はじめに
この節では基線を使った分割法の作図原理や使用例について説明します。
1~3点透視の各章に設けてある「増殖と分割」の節でも作図手順の説明はしていますので、そちらも併せて参照してください。
(本節で説明する分割法は、増殖法も含んでいます。元々「増殖と分割」は「拡大と縮小」のようなもので、操作自体に本質的な違いはありません)
関連ページ
1点透視 - 増殖と分割
2点透視 - 増殖と分割
3点透視 - 増殖と分割
前提知識
本サイトの構成は前章以前をすべて理解しているという前提で成り立っているため、あえて書くべきかどうかは迷うところですが、この節は特に難易度が高いので前提が重要であることを強調したいと思います。 本節を読み進めるには、消失点と消失線に関する深い理解が必要です。(以下のコラムはとりあえず読み飛ばしても構いません。スライドの内容が理解できない場合は、読み返してみてください)
平面は直線の集合であり、消失線は消失点の集合です。空間上の直線Aとその消失点a、さらに平面Bとその消失線bについて、AがBに含まれるならばaもbに含まれ、AがBに含まれないならばaもbに含まれない、という法則が成り立ちます。
消失点を持たない直線は透視図法では常に重要な働きをします。なぜなら、消失点を持たない直線上に目盛りを取った場合、透視図上での目盛りの比率と実空間上での目盛りの比率が一致する性質があるからです。
消失点を持たない直線は、空間的に見るとPPと平行な直線です。あるいは観測者から見て同一の奥行にある点の集合と表現することもできます。 さらにこの直線は透視図上では、消失線と平行になるという重要な性質があります。ここでいう消失線とはその直線を含む平面の消失線のことです。
ある直線を含む平面は、その直線を軸として360°任意の方向に取ることができますが、面白いことにどの方向に取っても、それらの消失線は透視図上では全て平行線になります。これは軸となる直線がPPと平行であるが故の現象です。(軸となる直線がPPと平行でない場合、すなわち消失点を持つ直線である場合は、消失線群は平行にはならず消失点を中心とする放射線になります)
注意してほしいのは、この法則は逆に解釈しても成り立つということ。すなわち透視図上で適当に取った消失線に対し、その平行線を引いたとすると、自動的にその線はPPと平行になり、消失点を持たない直線になるという事実です。もちろん、その直線が対応する平面に含まれていることが絶対条件です。
透視図法において1本の直線を引くことを考える場合、描き手はその直線が空間的に見てどの方向を向いているか、あるいはどの平面に属しているかを把握している必要があります。この把握がおぼつかなくなると、自分は一体何を描いているのか、描き手自身が分からなくなってしまいます。 (本作図法は例外的に、作業用平面の3次元的な向きを描き手が把握していなくても問題ないという特徴を持ちますが、それでもある1つの平面上で作図していることだけは把握していなければなりません)
消失点 - 消失線
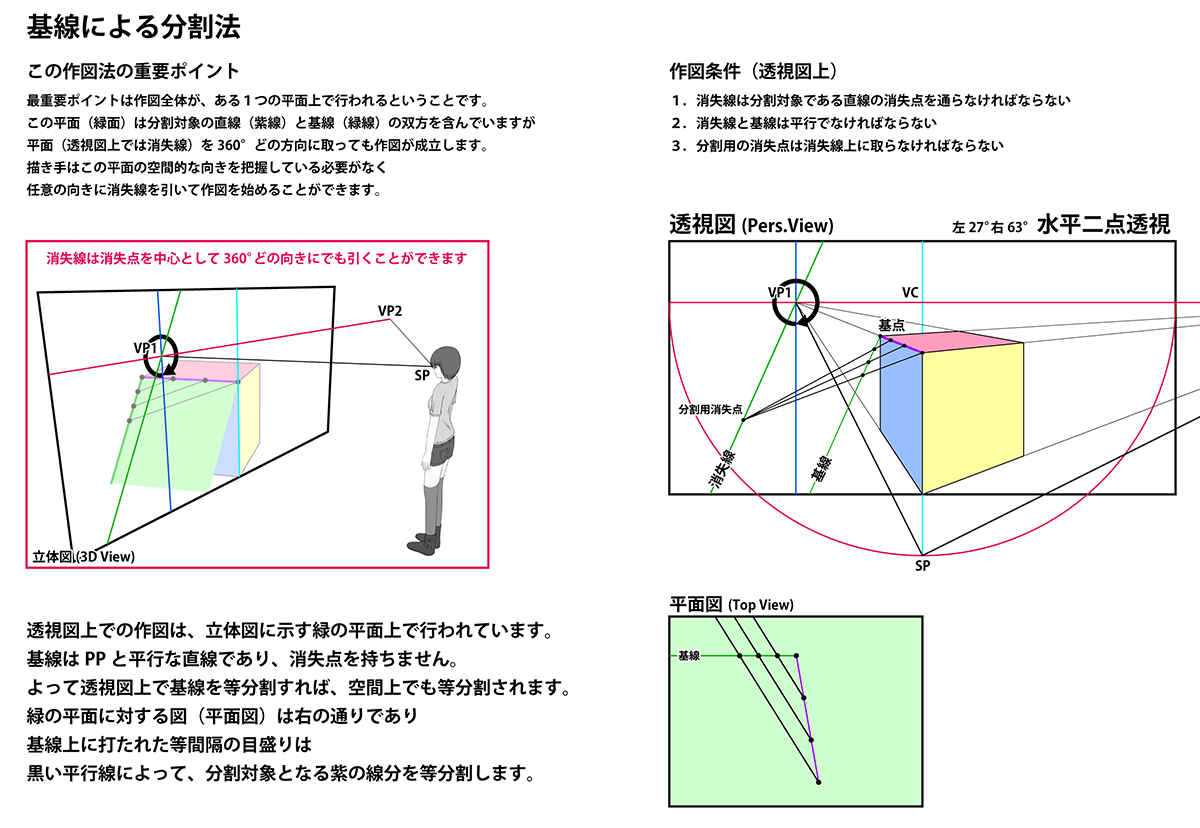
基線による分割法の作図原理
透視図法では実空間が持つ直交座標系の3軸に対して、その向きに応じて1点透視、2点透視、3点透視という分類をしますが、本作図法は1本の直線を対象として行うため、この分類は関係がありません。つまり何点透視であっても、あるいは○点透視という分類が不可能な場合であっても、本作図法は同様の手順で行うことができます。
まとめ
分割に使う消失線は360°どの方向でも可と表現していますが、例外的に分割対象直線と同じ向きの場合は作図不能です。(作業用平面上にSPが乗ってしまい、平面全体が直線として投影されるため、作図的に2直線の交点を得ることができなくなります)。 また分割対象直線と角度差がほとんどない場合や直交する場合も作図がしづらいです。実践で作図しやすい角度を探してみてください。
上図右上の3つの作図条件に関して補足します。(条件中の「消失線」とは作業用平面に対する消失線を指します)
- 仮に消失線が分割対象直線の消失点を含まないとすれば、対応する平面もまた分割対象直線を含むように取ることができないことを意味します。この作図法は作業用平面上に分割対象直線が乗ることで成立しますので、条件を満たさなければ作図法が破たんします。
- この作図法は基線上に取った目盛りの比率を分割対象直線に転写することを目的としています。目盛りを透視図上に直接作図するには、基線上の目盛りの比率と実空間上の目盛りの比率が一致する必要があります。つまり基線は消失点を持たない直線でなければならず、つまり基線が属する平面の消失線と平行でなければならないという結論になります。(平行でないということはどこかで消失線と交わるはずですので、消失点を持つことになります)
- この作図法はすべての作図線を作業用平面上に引きます。よってそれらの直線の消失点は作業用平面の消失線上に発生しなければならないと結論付けられます。
任意比率の転写
上記の作図法を応用すれば、パースのかかる直線上に任意比率の目盛りを打つことができます。 たとえば廊下の側面にできる窓や柱の間隔を図面をもとに正確に転写できます。 スライドで説明する予定でいますが、準備が整うまでお待ちください。(公開時期は未定です)