直交座標系における分類
透視図法の分類方法として「1点透視図」「2点透視図」「3点透視図」というものがありますが、 この分類の意味を正確に言い表すには、直交座標系という概念を説明する必要があります。
私たちの住む現実空間は「3次元」と呼ばれることがありますが、この3は何を意味しているのでしょうか。 簡単に言えば、ある空間は3つの数字の組み合わせでその位置を表すことができるということです。
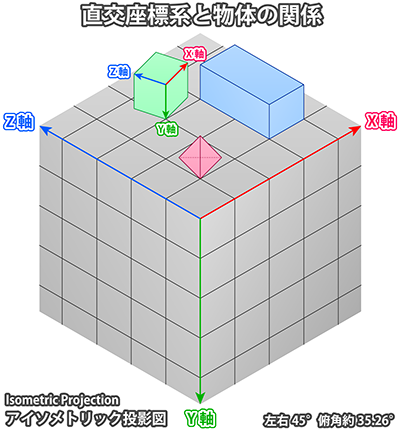
左図は空間をX軸、Y軸、Z軸の3つの要素で表現したものです。ここで重要なのは各軸が空間上で互いに直交し合っていうということです。 座標軸は必ずしも直交しなければならない性質のものではありませんが、普通は直交させておいた方がなにかと便利です。
空間を構成する座標軸(3次元の場合は3つ)のすべてが互いに直交し合っているとき、その座標系を直交座標系と呼びます。 そして透視図法における1~3点透視という分類は、物体が直交座標系の3軸に対して平行に配置されていることを前提としています。
青い直方体は空間全体を表す座標軸に沿っているので、1~3点透視という分類が可能です。 また緑の立方体は空間全体を表す座標軸に沿っていませんが、3組の辺が互いに直交していることに違いはないため、独自に座標軸を設定すれば、やはり1~3点透視という分類が可能です。
ところが赤い正三角錐は空間全体を表す座標軸に沿っておらず、それ以外の互いに直交し合う座標軸を定義したとしても、図形の形状的に座標軸に沿わせることができないため、1~3点透視という分類は不可能であると言えます。
1つ注意していただきたいのは、仮に分類不能であったとしても透視図法で描くことはできるということです。 ただ、座標軸に沿うものと比べると、複雑な角度の計算を要する場合があるため、作図の難易度は上がりがちです。
また緑の立方体のように空間全体の座標軸とは別の座標軸を設定することも、難易度としては高いといえます。
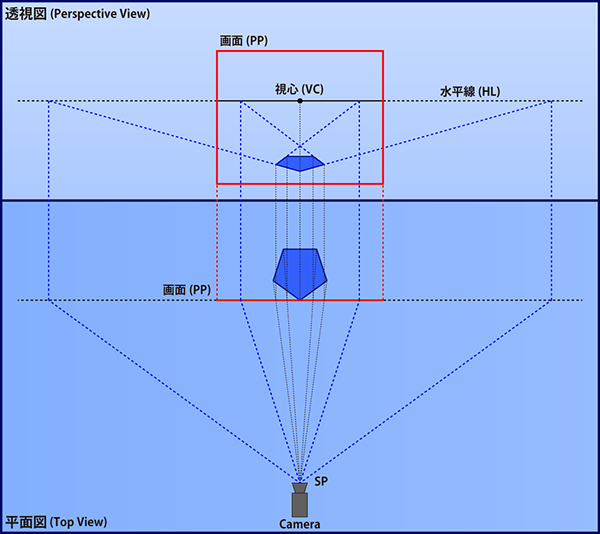
通常の透視図法の作図手順では、消失点の位置を適当に決めることが多いですが、
なぜそのようなことが許されるかというと、適当にとった消失点を直交座標系の3軸とみなせる視点(SP)が必ず存在するからです。
(3点透視図は一部条件あり)
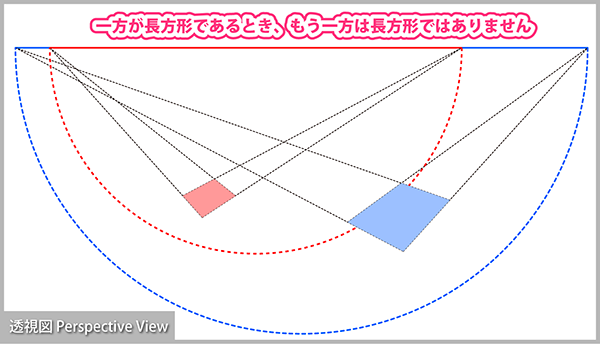
上図の四角形はいずれも2点透視図で描かれています。一見すると長方形のように見えますが、実はいずれか一方は確実に長方形でない平行四辺形だと言えます。 赤の四角形が長方形であるとすると、SPは赤破線上になければなりません。同様に青の四角形が長方形である条件は、SPが青破線上にあることです。 いずれか片方しか描かないのであれば、長方形とみなす視点が必ず存在すると言えますが、向きの異なる長方形を複数描く場合は、消失点を適当に取れるのは最初の1組だけであり、2組目以降は適当に取ることはできません。
これは座標軸であっても同じことであり、1個目の座標軸に関しては(3点透視図の場合は制約がありますが)消失点を適当に取ることができます。 ところが、同じ画面上に2つ以上の座標軸を設定する場合は、すでにSPの位置が確定している(90°視円錐が確定しているともいいます)ため、 90°視円錐が一致するような消失点の取り方をしなければなりません。 要するに座標軸を2つ以上設ける場合は、好き勝手に消失点を決められないということです。 (※詳細は応用の章で解説しています)
1~3点透視という分類は物体が直交座標系に沿うことを前提としていると述べましたが、実際問題として、その理屈を厳格に運用すると直方体以外の物体は分類不能という事態に陥ります。 そこである物体に対して全体を覆う直方体を考えることができるのであれば、その直方体をもって1~3点透視の分類に当てはめるのが通例です。
もっとも無理をすればどのような物体に対してもそれらを囲う直方体は定義できてしまいますので、その直方体が作画の補助として有効利用できるという条件が自動的に付加されることになります。 要するに全体を覆う直方体が、その中にある物体を描く際のガイド線として役に立つか否かで判断することになります。
また1枚の絵全体に対して「この絵は何点透視ですか?」と質問することがありますが、これは絵全体が概ねどの座標軸に沿っているかを考え、その座標軸とPPとの関係から○点透視である、と答えるのが一般的です。 このとき、多少の例外的な物体(空間全体の座標軸に沿わない物体)があっても、それらを無視して考えることになります。
○点透視図における消失点の数
先に述べた通り、直交座標系に沿う物体であれば、「1点透視図」「2点透視図」「3点透視図」のいずれかに分類できます。 いずれに分類されるかは、座標軸とPPの関係次第です。概要の章で説明した通り、直交座標系の3軸に対してPPと平行でない軸が1つの場合を1点透視、2つの場合を2点透視、3つの場合を3点透視と呼びます。 PPと平行でない軸(直線)は消失点を持ちますので、消失点の数は1点透視図であれば1個、2点透視図は2個、3点透視図は3個となります。
4点透視図というものは存在しません。なぜなら3次元空間において座標軸は3つしかないからです。 ○点透視の○は、直交座標系の3軸に対して消失点を持つ軸がいくつあるかを指す数字であり、描こうとしている図形が持つ消失点の数のことではありません。
例えば、正五角形を描く場合は消失点が5つ必要ですが、これを5点透視図とは呼びません。正五角形の場合、直交座標系の座標軸を設定できないので、分類不能といいます。 また、向きの異なる2点透視図の長方形を2個描く場合は、合計で4つの消失点が必要となりますが、これを4点透視図とは呼びません。 そうではなく2点透視図が2つあるといいます。
ただし魚眼レンズに関しては、理論上の画角が180°以上を持ちますので、直交座標系の1つの軸に対して、その両側に消失点が発生しえます。 よって最大で6点の消失点が発生することがあります。 しかし、それらを4~6点透視図と呼ぶ習慣があるか否かは定かではありません。 どちらにしても魚眼は透視図ではないので、透視図法としては3点透視が上限になります。
座標軸に沿わない場合
直交座標系の座標軸に沿わない物体を描く場合は、平行線の組の数だけ消失点を確保することになります。
例えば正五角形の場合は最大で5つの消失点を取ることで、正しい透視図を描くことができます。
下図は足線法によって作図された正五角形です。
この例では1つの辺がPPと平行であり消失点を持ちませんので、消失点の数は4個になります。