球
球はその中心が視心方向に存在する場合のみ正円となり、それ以外の場合は視心方向を対称軸とする楕円、放物線、双曲線のいずれかになります。
ほとんどの場合、球は楕円になると考えてよいでしょう。楕円として投影される場合、視心方向は必ず長軸となり、扁平率は視心から離れるほど大きくなります。
視心から等角度かつ同じ大きさの2つの球は、画面上で合同な図形(楕円、放物線、双曲線)になります。
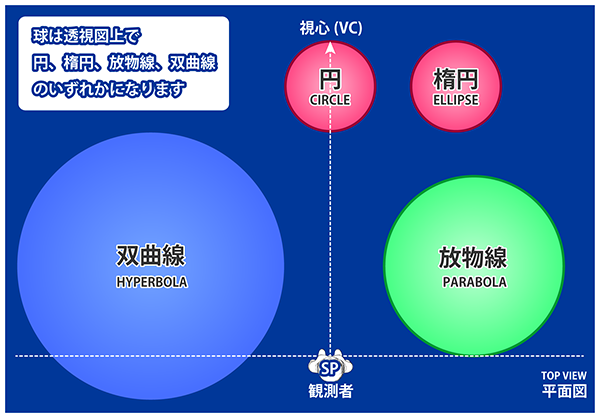
球の透視投影
この場合なにを描くかによりますが、単純に球の存在する箇所をすべて塗りつぶすのであれば、球は観測者からみて360°全方位に存在することになりますので、画面全体を塗りつぶすことになります。
空間的には球の外側にいて、平面図的に見ると円の内部にいる場合(たとえば、観測者が巨大な球の上に乗っている場合)は、立体的に見ればSPと球を結ぶ図形は円錐になりますので、透視図上では双曲線になります。
球の透視投影は円の透視投影とほぼ同じと考えられますが、物体とSPを結んだときにできる図形が常に直円錐になるという違いがあります。 (円はほとんどのケースで斜円錐になります)。 また円は直線になるケースが存在しましたが、球は厚みがあるため、絶対に直線にはなりません。
球の描き方1
SPと同じ高さに中心があり、SPから見て斜め前にいる球について考えます。 この球は空間的に見て、アイレベルを境に上下対称形であるため、透視図上でも水平線を境とした上下対称の図形になることが分かります。 必然的に楕円の軸は必ず視心方向を向くことになります。 またその軸が常に長軸となる理由ですが、これは足線法的に明らかです。 球は正面にいるときが最も短く投影され、斜めにいくほど長くなります。よって斜め前方向にある球は常に長軸が視心方向を向きます。
その他の向きについては、座標軸の回転によって説明が付きます。 球は(空間的に見て)視心を軸として回転したときと、平行移動させたときの形状が一致する特殊な図形です。 仮に(透視図上で)視心に対して真横を基準の向きとした場合、その他の向きにある球はカメラまたは世界を回転させることで常に真横にある状態に変換することができます。 よって、真横にいるときに長軸が視心方向を向くとすれば、斜めにいる球の楕円もやはり長軸が視心方向を向くことになります。 これは放物線や双曲線になる場合も同様であり、対称軸は常に視心方向を向きます。
外接立方体の上下左右の面に楕円を描いて、その幅を中に納まる球の楕円の幅とする作図法を上のスライドで示しましたが、以下に補足をします。 この作図法が成立するのは、立方体の面が空間的に見て視心と平行な場合に限ります。 言い換えると、平面図や側面図(あるいは視心と直交する任意の方向から見た図)で見たときに球の輪郭線としての円と立方体の面に描いた円がぴったり重なるときに限るということです。 つまり1点透視図の上下左右の面や水平2点透視図の上下の面がこれに該当します。 3点透視図には該当する面がありませんので、この方法は使えません。その場合は、立方体を1点透視図の向きになるように回転させてください。
球の描き方2(90°視円錐+足線法)
上のスライドでは立方体の側面に描いた楕円をガイドとする方法を示しましたが、2点および3点透視図のときは、立方体を回転する手間が侮れません。 次のスライドでは90°視円錐を利用した足線法による球の作図方法を説明します。 この作図法は外接立方体を必要とせず、画面上での球の中心と半径さえ図示できれば直接的に球を作図することができます。 空間に張られている座標軸を無視して作図するので、場が何点透視であっても関係なく、極めて少ない手数で完了する秀逸な方法です。
この作図法はあくまでも楕円を描く方法ですので、aは1未満の値でなければなりません。a=1のときは放物線であり、1を超えると双曲線になります。 bについては、0以上の任意の数を取ることができます。b=0のときは、球の中心が視心と一致しますので、正円になります。
PP(絵を描く領域)に対して90°視円錐が極端に大きい場合は、画角的に望遠であることを意味します。 このようなケースでは、楕円の長径と短径はそれぞれ半球の断面である正円とほぼ同じ径になります。 よって、単純に半球の断面に相当する正円を描いておけば、概ね正しい透視図と言えます。
ただし巨大な球の一部を描く場合など、球の大きさ自体が90°視円錐に対して十分大きい場合は、縮図を描くなどの方法で対応することになります。


