射影直線の配景写像
射影空間上のある射影平面(以下のスライドでは地面)が、任意の中心(同SP)によって別の射影平面(同PP)に投影されるとき、元の平面上の図形は、形を変えて投影されます。 このとき、元の図形と投影後の図形の対応関係を配景写像(perspective mapping)といいます。
透視図の定義によると、ある点の投影点はSPとその点を結んだ上でPPとの交点を求めるだけですので、観測者の前方か後方かに関わらず、投影点を求めることができます。 元々、射影幾何学における配景写像には、観測者の前方や後方という概念はなく、ある中心点に対する2つの平面間での図形の対応関係を指すだけなため、平面上の任意の点に対して、対応する点を求めることができます。 この考えは透視図上にも持ち込むことができ、作図上の補助線等に限れば観測者の後方であっても投影が可能です。 しかし絵画として考えると、観測者の後方にある物体は投影できないと言わざるをえません。
透視図法において投影対象となる空間は3次元であり、これに対して画面(PP)は2次元です。次元が1つ下がる関係上、ある投影点に対する元の点は無数に存在します。 よって透視図法で描かれる点は、空気のような透明な物質は無視するとして、基本的に観測者に最も近い1点だけになります。 ここに観測者の後方という世界を追加してしまうと、一体どの点を投影してよいか分からなくなってしまいます。 (魚眼レンズは観測者の前方と後方で投影点が異なるため、投影できます)
配景写像における点と点の対応関係は透視図の定義と同じものです。よって、透視図は配景写像そのものと言っても過言ではありません。 しかし両者に違いはあります。 配景写像には観測者の前方後方という概念がなく、平面上のすべての点をもう一方の平面に対応させることができます。 これは配景変換が平面から平面への変換であるが故です。これに対して、透視投影は空間から平面への変換です。
観測者の前後の問題はともかく、空間上の物体は多数の平面の集まりであると考えれば、多数の配景写像を行うことで透視図を得ることができます。 実際、3DCGはポリゴンと呼ばれる平面の組み合わせで立体を構成しており、ポリゴン単位で考えれば配景写像そのものといえます。 (あくまでも概念上の話であり、現実の実装は異なります)
上のスライドで説明した配景写像は2次元配景写像であり、一般にはn次元配景写像というものが存在します。例えば、1次元配景写像では平面上に中心Oと2つの直線L、L'を取り、その上にある点PとP'の写像を扱います。 ここで透視図法は空間を扱うのだから、3次元配景写像ではないか? という疑問が浮かび上がるかもしれませんが、透視図法は概念的には2次元配景写像と考えるべきです。
ここで問題となるのは3DCGの存在です。3DCGの基本原理はやはり透視投影ですが、実際に行われる演算は4×4行列を使った3次元射影変換(※)です。 「やはり透視投影は3次元ではないか!」と思われるかもしれませんが、話はそう簡単ではありません。
3次元射影変換の基礎となる3次元配景写像とは、3次元図形(直方体など)を他の3次元図形に移す写像のことであり、簡単に言うと3次元の物体を4次元空間に置き、任意の視点から3次元の写真を写すカメラで撮影したものです。 しかし4次元空間と言われても、直感的にイメージできる人は少ないと思います。これを通常の配景写像のモデルで図示しようとしても、直感的に分かりやすい図にはなりません。
※配景写像から派生した概念です。以下で説明します。3DCGにおける射影変換については、3DCGの節を参照してください。
配景変換と射影変換
ある図形Aと図形Bが配景写像の関係であるとき、AをBに変換することを配景変換(perspective transformation)と呼びます。 また配景写像を1回以上繰り返したものを射影写像(projective mapping)と呼び、同じく配景変換を1回以上繰り返したものを射影変換(projective transformation)と呼びます。 繰り返し回数は1回でも良いので、配景写像は射影写像の1種であり、配景変換もまた射影変換の1種です。 一般に配景変換や射影変換は逆変換が可能であり、すなわちBをAに変換することもまた配景変換(射影変換)です。
配景変換の概念は単純であり、簡単に言えば「ある平面図形をカメラで任意の視点から撮影したもの」と表現できます。また射影変換は、出来上がった写真を被写体にして再度撮影したものと解釈すれば良いです。
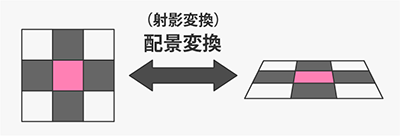
配景変換および射影変換には、以下の重要な法則があります。
- 点は点に、直線は直線に、曲線は曲線に変換されます。
- 多角形は同じ角数の多角形に変換されます。このとき頂点の順番は変化しません。
- 円錐曲線は円錐曲線に変換されます。
- 変換の前後で、点と線の関係は維持されますが、計量的性質(角度や長さ)は維持されません。
最後の項目については補足が必要でしょう。まず維持される性質について、いくつか例を挙げましょう。
- 直線Lと点Pに対して、それぞれが直線L'と点P'に変換されるとき、PがL上にあるならば、P'もまたL'上にあります。
- 2本の線(直線または曲線)がn個の交点を持つとき、変換後もn個の交点を持ちます。
- 曲線に対して引いた接線は、変換後も曲線に対する接線であり続けます。
逆に維持されない関係は何かというと、角度や長さなどの計量的性質です。 例えば2本の平行な直線は、変換後も平行であるとは限らず、基本的には平行にはなりません。 また円は中心からの距離が等しい点の集合ですが、配景変換において距離は維持されない性質であるため、 変換を掛けると楕円や放物線、双曲線になります。(例外的に円になるケースもあります)。 しかし計量的性質以外は保持されるため、円に接線を引いた場合、変換後も楕円等に対する接線になります。
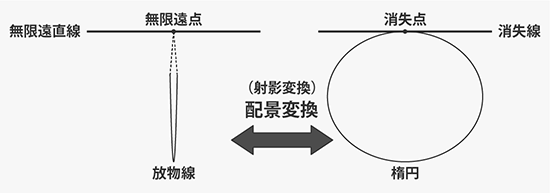
注意すべきは、これらの性質には無限遠点(あるいはその集合である無限遠直線)も含まれるということです。 無限の彼方まで伸びる放物線を地面に描き、これを頂点側からカメラで撮影すると、写真には水平線に接する楕円として写ります。 なぜなら放物線という図形は、無限遠直線と1点で交わる性質があるからです。(つまり無限遠直線は放物線の接線です)
これは直感的には分かりにくい性質です。放物線の左右の曲線はそれぞれ異なる方向を向いていますが、その傾きは最終的に限りなく対称軸と同じ方向を向きます。 よって左右の曲線は同一の無限遠点に収束します。これを透視図法で描くと、無限遠点は消失点に、無限遠直線は消失線に対応しますので、結果として消失線に接する楕円になります。 (透視図法的には左図は平面図、右図は透視図です)
次に説明する双曲線において、漸近線のなす角が0°になったものが放物線であると考えれば分かりやすいかもしれません。
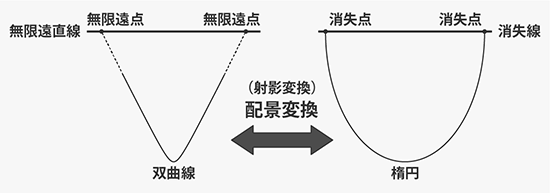
双曲線を同様に撮影すると、やはり楕円になります。ただし、双曲線の左右の曲線は無限の彼方では漸近線と同じ方向を向きますので、結果として左右の曲線は異なる消失点に収束します。 射影幾何学的には「双曲線は無限遠直線と2点で交わる」と言えます。
仮に撮影者の後方にも双曲線の残り半分(※)が描かれていたとすると、これらの無限遠点も前方に広がる曲線と同一点になります。(無限遠での曲線の方向は漸近線の方向と一致し、これは2方向しかないので無限遠点は2つになります)。 このとき水平線の上部にも楕円の半分が投影され、上の楕円も消失点を共有することから、結果として完全に閉じた1つの楕円になります。 また撮影者が対称点(すなわち漸近線の交点)上に立っていた場合は、透視図上の楕円も水平線を境に対称となります。 (つまり一般的に上下対称になるわけではないです)
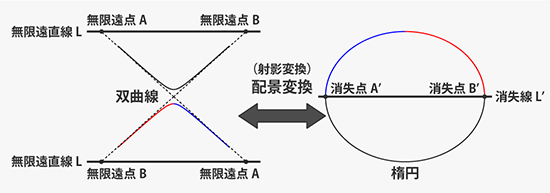
※本来、双曲線は2本の曲線を1組とする図形です。
透視図法では円が直線として見えるケースが存在しますが、配景写像における中心は2つの平面上にない点を取るのがルールであるため、平面全体が直線として投影されることはありません。 よって曲線は必ず曲線になります。なお、2つの平面を平行に取ることは許されています。この場合、写像は相似になります。
配景の中心を平面上に取れない理由ですが、平面上に中心を取ると一方の平面全体が、もう一方の平面に直線または点として投影されてしまい、写像の可逆性が失われてしまうからです。 配景写像(変換)や射影写像(変換)はいずれも可逆であり、写像の用語でいうところの全単射です。 つまりある1枚の画像全体に対して任意の射影変換をかけたとすると、元の画像に戻すための逆変換が必ず存在します。 言い換えると、変換によって画素の情報は一切失われないことを意味します。(あくまでも数学上の話です)
ある2本の直線が平行であるとは、その直線が同一平面上に存在し、かつ直線をどこまで延長しても交わらないことを指します。 しかし射影幾何学における射影直線は、通常の概念において平行な状態であったとしても無限遠点という交点を持つため、厳密に言うと射影空間には平行な直線は存在しません。
とはいえ、説明のたびに「無限遠点以外で交点を持たない直線」などの表現を使うのは冗長であるため、この章において単に平行と述べた場合は「無限遠点以外で交点を持たない直線」すなわち「ユークリッド空間における平行」を指すものとします。
両者の違いを厳密に区別するのは難しいのですが、変換とは自分自身への写像を指します。 例えば、直線Lと直線L'があるとき、「Lの射影変換をf、L'の射影変換をf'とするとき、f'○φ=φ○fを満たすφが存在するならば、2つの射影変換fとf'は射影的に同値、つまり本質的に同じ変換である。ただしφはLからL'への射影写像とする」と言った表現をします。 イメージとしては、写像は自身を変化させず、一方から他方に移すのに対し、変換は自分自身を書き換えます。


