
1.遠近法
透視図(perspective diagram)
透視投影によって作られる図を透視図と呼びます。 透視図は人間の視覚によって得られる像に非常に近いと言われており、 今日存在する絵画や写真、3DCGでの空間表現は、そのほとんどが透視投影を原理としています。
パース(perspective)
日本語では「遠近法」や「透視図法」を指して、「パース」と呼ばれることが一般的です。 また透視図法的な遠近感が付くことを俗に「パースがかかる」と言い、遠近感の表現が適切でない場合を「パースが狂う」「パースがおかしい」と言うことがあります。
語源は英語のperspectiveであり、こちらも「遠近法」に匹敵する広い意味を持つ単語です。linear perspectiveと言った場合は「透視図法」に限定されます。
遠近法(perspective)
物体の遠近を表す手法を総称して遠近法と呼びます。透視図法は線遠近法とも呼ばれ、遠近法の代表格です。 最大の特徴は「遠くのものほど小さく見える」ことですが、遠近法という言葉自体はより広い意味を持つため、必ずしもこの特徴を持つものに限定されるわけではありません。 一例として空気遠近法が挙げられます。簡単に言うと「遠くのものほど薄く描く」技法であり、ぼかしや霞みがかった表現を行います。 各種遠近法は単体で使うとは限らず、線遠近法と空気遠近法を併用することも多々あります。
視点を無限遠に置く平行投影図は、空間上での位置に関係なく同じ大きさの物体が同じ大きさで描かれるため、 一般的には「遠近感が付かない」とされますが、視線の角度によっては前後関係が分かる場合もあり、広い意味では遠近法と呼べるかもしれません。 実際、平行投影図は視点の遠い透視図とみなせますので、厳密な意味で両者を切り分けるのは困難だと言えます。
線遠近法(linear perspective)
透視図法の別名です。線遠近法は空間上での直線が画面上でも直線になるという特徴を持ちます。 一見当たり前のように映る性質ですが、遠近法においてこれを満たすものは透視図と平行投影図ぐらいしか存在せず、 他の遠近法(魚眼やパノラマなどが代表)では直線が曲線として描写されます。
透視図法の欠点とされる広角による歪みは直線性を維持するための代償であり、歪みをなんらかの手段で改善するには直線性を捨てるしかありません。 しかし直線が曲がることもまた歪みなため、究極的な解決策はないと言えます。
| 線遠近法(透視図) | 曲線遠近法(天使遠近法) |
|---|---|
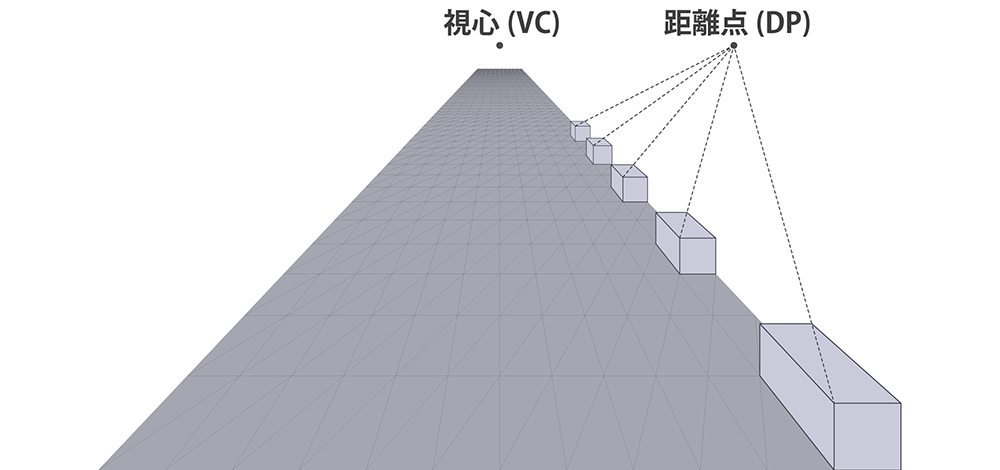 |
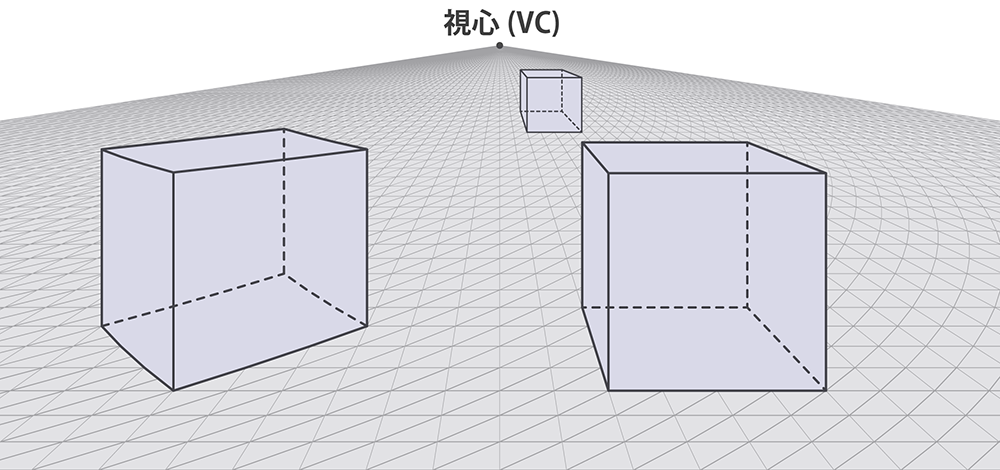 |
| 広角領域ほど歪みが強くなりますが、直線性を維持するにはこれを受け入れるしかありません。 | 広角領域の歪みを無理やり改善したものです。その代償として視心方向以外の直線性は失われます。 |
2.直交座標系
○点透視
実空間上に1つの直方体を配置したとき、平行な辺の組は3組あります。 このうち視線の向きと直交しない組が1組の場合を、1点透視、 2組の場合を2点透視、3組の場合を3点透視と呼びます。 物体が直方体でない場合は、外接する直方体などに置き換えて考えます。 1~3点透視は1枚の絵の中に混在させることができます。
1点透視(one point perspective)
1点透視では1つの直方体に対し、消失点がただ1つ発生します。また消失点は必ず視心と一致します。
2点透視(two point perspective)
2点透視では1つの直方体に対し、2つの消失点が発生します。2つの消失点はSPから見て90°の角度差を持ちます。
3点透視(three point perspective)
3点透視では1つの直方体に対し、3つの消失点が発生します。3つの消失点から任意の2つを選んだとき、2つの消失点はSPから見て90°の角度差を持ちます。
3.図法的要素
観測者(observer)
透視図とは端的に表現すると「誰かの視界を切り取ったもの」に相当し、その誰かを観測者と呼びます。透視図法の用語として正式に定義されているか否かは定かではありません。
画面(picture plane、略記PP)
実空間上の物体を投影するための仮想の平面です。投影面とも呼ばれます。この面に投影される像が透視図です。 透明のガラスをイメージしてください。視点を固定した上でガラスに映る像を忠実になぞっていけば、透視図が完成します。 画面は常に視線の向き(視心)と直交します。
視点(station point、略記SP)
観測者の目の位置(カメラではレンズの主点位置)の3次元座標を指します。 透視図は視点と物体を直線で結ぶことで投影位置を求めるため、視点の位置を把握することは作図上の重要課題になります。
立点(standing point、略記SP)
観測者の足元を意味します。平面図では視点と立点が同一位置にプロットされます。 本サイトでは視点と立点を厳密に区別せず、立点と表記している場合があります。
視円錐(visual cone)
観測者の視野の広がりを円錐で表現したものが視円錐です。
視円錐は画面の大きさを決める際に、ガイドとして利用できます。
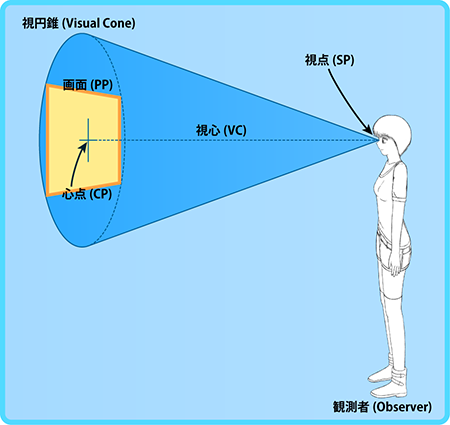
視心(visual center、略記VC)
人間やカメラの視野は便宜上円錐に例えられることがあります。 すなわち、視野は一定の範囲を持ちます。視心は視野の中心方向を指す言葉であり、 図形的に言えば、視円錐の中心軸のことです。
心点(central point、略記CP)
心点とは、視心と画面の交点のことです。 しかし当サイトでは、心点と視心を厳密に区別せず、どちらも視心(VC)と表現しています。 本来、視心は方向を示す言葉であるため、図形で表せば直線であり、この直線と画面との交点が心点です。 一般的なカメラで撮影された写真の場合、(トリミングしていなければ)画像中央が心点になります。
アイレベル(eye level, 略記EL)
地面を基準としたカメラの高さ(観測者の目の高さ)です。 カメラを上下に傾けた場合も概念は変わりません。 カメラからの距離に関係なくアイレベルと同じ高さにあるすべての点は水平線上に現れる性質があります。
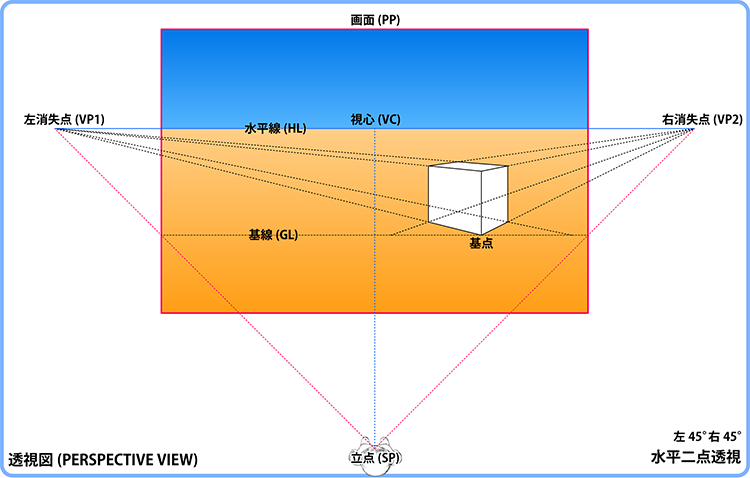
基点
ある物体を作図する上で、基準となる点です。基点は基線上に取ります。 立方体を描く場合、立方体の手前の頂点のうち地面に接する点を基点とすることが通例です。
基線(ground line, 略記GL)
地面線ともいいます。
ある物体を作図する上で、基準となる奥行を指す直線です。通常は地面上に引きますが、地面と平行であれば、空中に引くこともできます。
基線は消失点を持たない直線であるため、透視図上では必ず水平線と平行な方向に引きます。
地面(ground plane)
アイレベルの基準となる平面のことです。透視図法では、描き手の都合の良い面を「地面」として設定できます。
水平線(horizon line, 略記HL)
地面は無限の彼方では直線で表現されます。これが水平線です。(日本語では地平線と呼ぶこともありますが、英語では両者ともhorizonと表現します)。 水平方向の1点透視図や2点透視図では視心および消失点が水平線上に現れます。
垂直線(vertical line)
水平線と同じ概念ですが、垂直方向に現れるのが垂直線です。(本サイトでは所々で使用していますが、パース用語としては定義されていなかったと思います)。 カメラを90度傾ければ、水平と垂直は入れ替わります。すなわち水平に対して成り立つ法則は垂直に対しても成り立ちます。
消失点(vanishing point, 略記VP)
実空間上に並ぶ直線を奥行方向に伸ばすと、無限遠で消失点に到達します。 実空間上で平行な直線は、同一の消失点を持つという特徴があります。 消失点は視心とのなす角によってその位置が決定します。 画面上での視心からの距離は正接(タンジェント)に比例します。
消失線(vanishing line)
消失点を2次元に拡張した概念です。つまり実空間上の平面を奥行方向に伸ばしたとき、無限遠に発生する直線を指します。 平行な平面同士は、同じ消失線に収束します。 消失線は消失点の集合と考えることもでき、ある平面上の平行でない2直線に対する消失点を求めることができれば、それらを結んでできる線がその平面の消失線になります。
対角消失点(diagonal vanishing point, 略記DVPまたはDP)
パース用語として明確な定義があるかは定かではないですが、本サイトでは「正方形の対角線が作る消失点」の意味で使用しています。 基本的には距離点と同じ意味になるはずですが、距離点という用語が1点透視以外でも使用できるか否かが分かっていません。 特に1点透視と2点透視を混在させた図の場合、何をもって距離点と定義するのかが不明瞭です。 本サイトでは地面と平行かつ視心に対して45°をなす方向の消失点を距離点と定義しています。したがって、2,3点透視図での正方形の対角消失点は 距離点とは一致しません。
距離点(distance point, 略記DP)
D点とも呼ばれます。地面と平行かつ視心に対して45度をなす直線の消失点を指します。1点透視図では、この消失点を利用することにより奥行方向の正方形を作画できます。
測点(measuring point, 略記MP)
M点とも呼ばれます。ある消失線上の1個の消失点と対応する消失点であり、これを利用して二等辺三角形を作図できます。 応用すれば、任意の辺をパースのかからない向きまで回転させること(あるいはその逆)ができ、任意の長さを正確に測ることが可能になります。 また2点透視図では、測点を利用して高さ方向に傾斜を持つ直線の消失点を求めることもできます。


