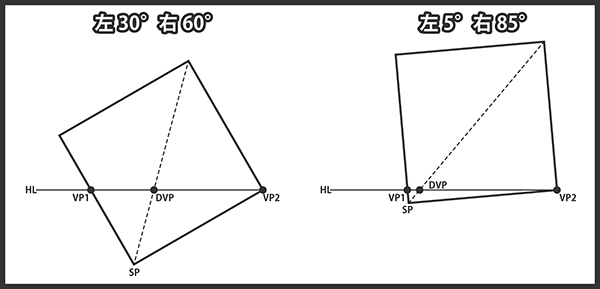
スライドのPAGE3で長方形の辺の比が不明なとき、視心とSPが特定できないと示しました。 これは求め方が分からないという意味ではなく、両者を一意に定める手段が存在しないことを証明できるという意味です。 簡単に説明すると、こうです。 線分VP1-VP2の両端を除く任意の点を視心としたとき、対応するSPは視心を通る水平線の垂線とVP1-VP2を直径とする円の交点として得ることができます。 このとき、４点SP,VC,VP1,VP2は数学的な整合性が取れており、画角的に不適切なものになることはあっても、空間の解釈として破綻することはありません。 これは視心を一意に定められないことを意味します。

つまり適当に取った２つの消失点だけでは、数学的に視心を求める方法は絶対に存在しないということです。この場合、視心は描き手が決めるしかありません。 特にこだわりがないのであれば、水平線上かつ画面の中央付近に視心を置くのが無難です。 ただし視心を明確に定めないまま、寸法が既知の何かを画面上に置けば、その瞬間に視心が確定してしまうので、その場合は描き手が視心の位置を勝手に決めることはできません。

みなせます。スライドのP13に示す図から予測が可能ですが、対辺が平行でなく、すべての内角が180°未満の四角形であれば、どのような四角形であっても二点透視図の正方形とみなす視点(SP)が存在します。 ある水平線上にVP1,VP2を適当に置き、２点間にDVPをやはり適当に置いたとすると、これに対応する正方形の向きが必ず存在することは、下図から読み取れるかと思います。

さらに二点透視図に限らない一般論として言えば、任意の正方形Ａに対して、内角が180°未満で構成される任意の四角形Ｂを用意したとき、実空間上でＡである図形が透視図上でＢに見える視点は必ず存在します。 ただしここでいう透視図とはカメラを無限遠まで離した平行投影図も含むものとします。

実際には適正画角というものがありますので、適当に四角形を描いておけばOKとはなりませんが、ある程度見た目で判断して四角形を描き、それを描き手が正方形と主張することは可能です。もちろん制約のない（視心やSPが確定していない）画面での話です。

例	図形	座標系	カメラ距離	解説
	正方形	１点透視	有限または無限	空間上での正方形が透視図上でも正方形に見える視点は、１点透視図に限られます。カメラと被写体との距離は有限でも無限でも構いません。
	長方形	２点透視	無限	正方形が長方形に見える視点は、２点透視図のカメラを無限遠に離した場合に限ります。
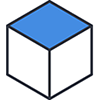	菱形	３点透視	無限	正方形が菱形に見える視点は、消失点が二等辺三角形（正三角形を含む）を描く３点透視図のカメラを無限遠に離した場合に限ります。
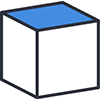	平行四辺形	３点透視	無限	正方形が平行四辺形に見える視点は、任意の３点透視図のカメラを無限遠に離した場合に限ります。
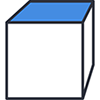	台形	１点透視 ２点透視	有限	正方形が台形に見える視点は、有限距離の１点透視図または２点透視図に限ります。
	その他	２点透視 ３点透視	有限	正方形が平行対のない四角形に見える視点は、カメラ距離が有限の２点透視図または３点透視図に限ります。

みなせません。地面に正方形（見かけ上は普通の四角形）を描いた瞬間に高さ方向の辺の長さは一意に決まるので、測点法などを使って長さを測る必要があります。