視心をまたぐ90度の関係を持つ2消失点の角度
2点透視図で困るのは、ラフで描いた絵のSP位置を逆算する場合です。一般的な作図手順では、2つの消失点を直径とする円を描かなければなりませんが、通常この円はとても巨大なものとなるため、アナログ環境では作画が厳しいと思います。そこでこの節では、円を描かずにSPの位置を計算で求める方法を示したいと思います。
3点透視の消失点が正三角形になる条件
3点透視図で3つの消失点を結んでできる図形が正三角形となる条件を考えます。
平面図としての角度については、水平線上の左右の消失点が視心に対して同角度かつ足して90度の関係でなければならないことから、左右共に45度をなしていなければならないことが分かります。
ところが仰俯角に関しては、消失点(VP3)と消失線(VP1-VP2)の間に発生する関係なため、上下が同じ角度とはならず約35.26度となります。
(値が異なるのは測る角度の違いによるもので、3つの消失点や3本の消失線は図形的に見れば均衡しています)
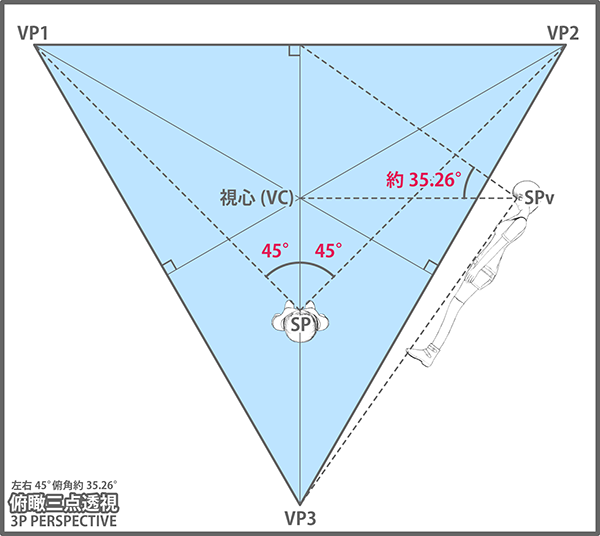
ここで正三角形パターンにおける仰俯角は、上のスライド「視心をまたぐ90度の関係を持つ2消失点の角度」におけるa:b=1:2となるときの角度に等しく
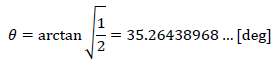
で計算できます。これは立方体を対角線で2等分した際に現れる断面の長方形の対角線角度に等しいです。
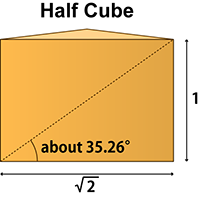
なおこの角度の関係を維持したまま、カメラを無限遠まで離すと、アイソメトリック投影(3点透視図をベースとした平行投影図の一種)となります。 平行投影は意外と難度が高いので、応用の章(あるいは専用の章)での解説を予定しています。
3消失点が正三角形パターンになる場合の仰俯角は約35.26°で正しいのですが、1度未満の角度を表す方法には注意を払う必要があります。 1度=60分とする六十分法を使う場合、端数である約0.26度は約16分となります。 よって、35.26度は35度16分と表現することもできます。分は記号で描く場合は'を使うので、35°16'と書くことになります。


